
【题目】已知函数y=f(x),若在定义域内存在x0 , 使得f(﹣x0)=﹣f(x0)成立,则称x0为函数y=f(x)的局部对称点.
(1)若a、b∈R且a≠0,证明:函数f(x)=ax2+bx﹣a必有局部对称点;
(2)若函数f(x)=2x+c在定义域[﹣1,2]内有局部对称点,求实数c的取值范围;
(3)若函数f(x)=4x﹣m2x+1+m2﹣3在R上有局部对称点,求实数m的取值范围.
【答案】
(1)证明:由f(x)=ax2+bx﹣a得f(﹣x)=ax2﹣bx﹣a
代入f(﹣x)+f(x)=0得,(ax2+bx﹣a)+(ax2﹣bx﹣a)=0,
得到关于x的方程ax2﹣a=0(a≠0),
其中△=4a2,由于a∈R且a≠0,所以△>0恒成立
所以函数f(x)=ax2+bx﹣a(a≠0)必有局部对称点
(2)证明:方程2x+2﹣x+2c=0在区间[﹣1,2]上有解,于是﹣2c=2x+2﹣x
设t=2x(﹣1≤x≤2), ![]() ,
, ![]() 其中
其中 ![]()
所以 ![]()
(3)证明:f(﹣x)=4﹣x﹣m2﹣x+1+m2﹣3,
由于f(﹣x)+f(x)=0,所以4﹣x﹣m2﹣x+1+m2﹣3=﹣(4x﹣m2x+1+m2﹣3)
于是(4x+4﹣x)﹣2m(2x+2﹣x)+2(m2﹣3)=0(*)在R上有解
令2x+2﹣x=t(t≥2),则4x+4﹣x=t2﹣2,
所以方程(*)变为t2﹣2mt+2m2﹣8=0在区间[2,+∞)内有解,需满足条件: 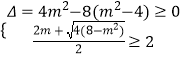
即 ![]() ,
,
化简得 ![]()
【解析】(1)根据局部对称点的定义,结合已知中二次函数的图象和性质,可证明得结论;(2)若函数f(x)=2x+c在定义域[﹣1,2]内有局部对称点,则方程2x+2﹣x+2c=0在区间[﹣1,2]上有解,解得实数c的取值范围;(3)若函数f(x)=4x﹣m2x+1+m2﹣3在R上有局部对称点,则方程(4x+4﹣x)﹣2m(2x+2﹣x)+2(m2﹣3)=0(*)在R上有解,解得实数m的取值范围.
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减才能正确解答此题.
上递减才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】双曲线C的中心在原点,右焦点为 ![]() ,渐近线方程为
,渐近线方程为 ![]() .
.
(1)求双曲线C的方程;
(2)设直线l:y=kx+1与双曲线C交于A、B两点,问:当k为何值时,以AB为直径的圆过原点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小张在淘宝网上开一家商店,他以10元每条的价格购进某品牌积压围巾2000条.定价前,小张先搜索了淘宝网上的其它网店,发现:A商店以30元每条的价格销售,平均每日销售量为10条;B商店以25元每条的价格销售,平均每日销售量为20条.假定这种围巾的销售量t(条)是售价x(元)(x∈Z+)的一次函数,且各个商店间的售价、销售量等方面不会互相影响.
(1)试写出围巾销售每日的毛利润y(元)关于售价x(元)(x∈Z+)的函数关系式(不必写出定义域),并帮助小张定价,使得每日的毛利润最高(每日的毛利润为每日卖出商品的进货价与销售价之间的差价);
(2)考虑到这批围巾的管理、仓储等费用为200元/天(只要围巾没有售完,均须支付200元/天,管理、仓储等费用与围巾数量无关),试问小张应该如何定价,使这批围巾的总利润最高(总利润=总毛利润﹣总管理、仓储等费用)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有![]() (n≥2,n∈N*)个给定的不同的数随机排成一个下图所示的三角形数阵:
(n≥2,n∈N*)个给定的不同的数随机排成一个下图所示的三角形数阵:

设Mk是第k行中的最大数,其中1≤k≤n,k∈N*.记M1<M2<…<Mn的概率为pn.
(1)求p2的值;
(2)证明:pn>![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于点E. 
(1)若D为AC的中点,证明:DE是⊙O的切线;
(2)若OA= ![]() CE,求∠ACB的大小.
CE,求∠ACB的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com