Question

【题目】如图，已知与圆相切于点，经过点的割线交圆于点，的平分线分别交于点.

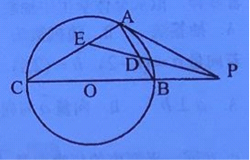
（1）证明：;

（2）若，求的值.

Answer 1

【答案】（1）证明见解析；（2）

【解析】

试题分析：（1）要证两角相等，与已知条件“是角平分线”联系，这两个分别都可以作为一个三角形的外角，∠ADE=∠BAP+∠APD,∠AED=∠C+∠CPE，而由角平分线有，∠APD=∠CPE，由切线的性质有∠BAP=∠C，因此结论得这两点；（2）由切线性质可得APC∽BPA，这样会出现线段的比值，再由及（1）的证明知中，，从而求得．

试题解析：（1）∵PA是切线，AB是弦，∴∠BAP=∠C

又∵∠APD=∠CPE,∴∠BAP+∠APD=∠C+∠CPE.

∵∠ADE=∠BAP+∠APD,∠AED=∠C+∠CPE.

∴∠ADE=∠AED

（2）由（1）知∠BAP=∠C,又∠APC=∠BPA,∴APC∽BPA， ，

∵AC=AP, ∠BAP=∠C=∠APC,

由三角形的内角和定理知：∠C+∠APC+∠PAC=180,

∵BC是圆O的直径,∴∠BAC=90,∴∠C+∠APC+∠BAP=90,∴∠C=∠APC=∠BAP=30,

在RtABC中,,∴