
【题目】函数![]() 有两个零点,则
有两个零点,则![]() 的取值范围为( )
的取值范围为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
要使函数f(x)=xln x- m有两个零点,即xlnx=m有两个不同的根,即函数y= g (x)的图像与直线y = m的图像有两个不同的交点,设g(x)= xln x,对其求导分析单调性,进而表示极小值,再由极限思想考虑端点值,最后由数形结合思想观察图象得答案.
函数的定义域为(0, +∞),由f(x)=xlnx一m=0,得xlnx=m,
设g(x)=xlnx,则g'(x)=lnx+1,
由g'(x)>0,得![]() ,此时函数g (x)单调递增;
,此时函数g (x)单调递增;
由g'(x)<0,得0<x<![]() ,此时函数g(x)单调递减;
,此时函数g(x)单调递减;
即当x=![]() 时,函数g (x)取得极小值
时,函数g (x)取得极小值![]()
当x→0,g(x)→0;当x→+∞,g(x)→十∞,
所以要使函数f(x)=xlnx-m有两个零点,即xlnx=m有两个不同的根,即函数y=g(x)的图像与直线y=m的图像有两个不同的交点,
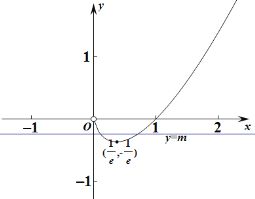
则-![]() < m< 0,
< m< 0,
故选:A


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】某保险公司为客户定制了5个险种:甲,一年期短险;乙,两全保险;丙,理财类保险;丁,定期寿险:戊,重大疾病保险,各种保险按相关约定进行参保与理赔.该保险公司对5个险种参保客户进行抽样调查,得出如下的统计图例,以下四个选项错误的是( )
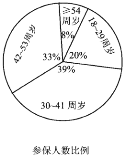
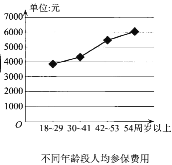
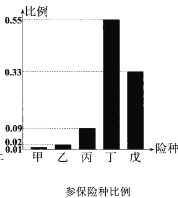
A.54周岁以上参保人数最少B.18~29周岁人群参保总费用最少
C.丁险种更受参保人青睐D.30周岁以上的人群约占参保人群的80%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】4月23日是“世界读书日”,某中学开展了一系列的读书教育活动.学校为了解高三学生课外阅读情况,采用分层抽样的方法从高三某班甲、乙、丙、丁四个读书小组(每名学生只能参加一个读书小组)学生抽取12名学生参加问卷调查.各组人数统计如下:
小组 | 甲 | 乙 | 丙 | 丁 |
人数 | 12 | 9 | 6 | 9 |
(1)从参加问卷调查的12名学生中随机抽取2人,求这2人来自同一个小组的概率;
(2)从已抽取的甲、丙两个小组的学生中随机抽取2人,用![]() 表示抽得甲组学生的人数,求随机变量
表示抽得甲组学生的人数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在①![]() .②
.②![]() 的面积
的面积![]() ,③
,③![]() 这三个条件中任选一个,补充在下面问题中,问题中的
这三个条件中任选一个,补充在下面问题中,问题中的![]() 是否为等边三角形,请说明理由.在
是否为等边三角形,请说明理由.在![]() 中,
中,![]() 分别为内角
分别为内角![]() 的对边,且
的对边,且![]() ,________,试判断
,________,试判断![]() 是否为等边三角形?(注:如果选择多个条件分别解答,按第一个解答计分)
是否为等边三角形?(注:如果选择多个条件分别解答,按第一个解答计分)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2017年1月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论正确的是( )
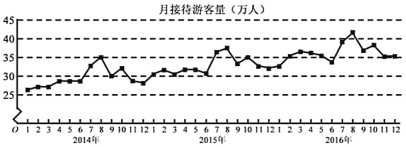
A.月接待游客逐月增加
B.年接待游客量逐年减少
C.各年的月接待游客量高峰期大致在6、7月
D.各年1月至6月的月接待游客量相对于7月至12月,波动性较小,变化比较稳定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的有_________(填序号)
①已知![]() :
:![]() 或
或![]() ,
,![]() :
:![]() ,则
,则![]() 是
是![]() 的必要不充分条件;
的必要不充分条件;
②“![]() ”是“函数
”是“函数![]() 的最小正周期为
的最小正周期为![]() ”的充分不必要条件;
”的充分不必要条件;
③![]() 中,内角
中,内角![]() ,
,![]() ,
,![]() 所对的边分别为
所对的边分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,则“
,则“![]() ”是“
”是“![]() 为等腰三角形”的必要不充分条件;
为等腰三角形”的必要不充分条件;
④若命题![]() :“函数
:“函数![]() 的值域为
的值域为![]() ”为真命题,则实数
”为真命题,则实数![]() 的取值范围是
的取值范围是![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com