
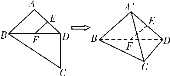
【题目】如图,平面四边形ABCD中,E、F是AD、BD中点,AB=AD=CD=2, BD=2![]() ,∠BDC=90°,将△ABD沿对角线BD折起至△
,∠BDC=90°,将△ABD沿对角线BD折起至△![]() ,使平面
,使平面![]() ⊥平面BCD,则四面体
⊥平面BCD,则四面体![]() 中,下列结论不正确是 ( )
中,下列结论不正确是 ( )
A. EF∥平面![]()
B. 异面直线CD与![]() 所成的角为90°
所成的角为90°
C. 异面直线EF与![]() 所成的角为60°
所成的角为60°
D. 直线![]() 与平面BCD所成的角为30°
与平面BCD所成的角为30°
【答案】C
【解析】
根据线线平行判定定理、异面直线所成角、直线与平面所成角等知识对选项A、B、C、D进行逐一判断其正确与否.
解:选项A:因为E、F是AD、BD中点,
所以![]() ,
,
因为![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
所以EF∥平面![]() ,
,
所以选项A正确;
选项B:因为平面![]() ⊥平面BCD,
⊥平面BCD,
平面![]()
![]() 平面BCD
平面BCD![]() ,
,
且∠BDC=90°,即![]() ,
,
又因为![]() 平面BCD,
平面BCD,
故![]() 平面
平面![]() ,
,
故![]()
![]() ,
,
所以异面直线CD与![]() 所成的角为90°,
所成的角为90°,
选项B正确;
选项C:由选项B可知![]() 平面
平面![]() ,
,
所以![]()
![]() ,
,
因为AD=CD=2,
即![]() =CD=2,
=CD=2,
所以由勾股定理得,![]() ,
,
在![]() 中,
中,
BC=![]() ,
,
在![]() 中,
中,
![]() ,
,
故![]() ,即
,即![]() ,
,
因为![]() ,
,
所以![]() ,
,
故选项C错误;
选项D:连接![]()
因为![]()
所以![]()
因为![]() 是中点,
是中点,
所以![]() ,
,
因为平面![]() ⊥平面BCD,
⊥平面BCD,
平面![]()
![]() 平面BCD
平面BCD![]() ,
,
又因为![]() 平面
平面![]() ,
,
故![]() 平面
平面![]() ,
,
所以![]() 即为直线
即为直线![]() 与平面BCD所成的角,
与平面BCD所成的角,
在![]() 中,
中,![]() ,
,![]() ,
,
所以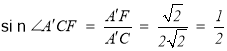 ,
,
所以![]() ,
,
故直线![]() 与平面BCD所成的角为30°,
与平面BCD所成的角为30°,
故选项D正确,
本题不正确的选项为C,故选C.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:
【题目】在“新零售”模式的背景下,某大型零售公司推广线下分店,计划在S市的A区开设分店,为了确定在该区开设分店的个数,该公司对该市已开设分店的其他区的数据作了初步处理后得到下列表格.记x表示在各区开设分店的个数,y表示这个x个分店的年收入之和.

(1)该公司已经过初步判断,可用线性回归模型拟合y与x的关系,求y关于x的线性回归方程![]()
(2)假设该公司在A区获得的总年利润z(单位:百万元)与x,y之间的关系为![]() ,请结合(1)中的线性回归方程,估算该公司应在A区开设多少个分店时,才能使A区平均每个分店的年利润最大?
,请结合(1)中的线性回归方程,估算该公司应在A区开设多少个分店时,才能使A区平均每个分店的年利润最大?
(参考公式:![]() ,其中
,其中 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 内,动点
内,动点![]() 与两定点
与两定点![]() ,
, ![]() 连线的斜率之积为
连线的斜率之积为![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设点![]() ,
, ![]() 是轨迹
是轨迹![]() 上相异的两点.
上相异的两点.
(Ⅰ)过点![]() ,
, ![]() 分别作抛物线
分别作抛物线![]() 的切线
的切线![]() ,
, ![]() ,
, ![]() 与
与![]() 两条切线相交于点
两条切线相交于点![]() ,证明:
,证明: ![]() ;
;
(Ⅱ)若直线![]() 与直线
与直线![]() 的斜率之积为
的斜率之积为![]() ,证明:
,证明: ![]() 为定值,并求出这个定值.
为定值,并求出这个定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥P﹣ABCD中,AD![]() BC,BC⊥CD,BC=CD=2AD=2,PD=
BC,BC⊥CD,BC=CD=2AD=2,PD=![]() ,侧面PBC是等边三角形.
,侧面PBC是等边三角形.
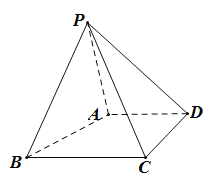
(1)证明:PA⊥平面PBC;
(2)求BC与平面PCD所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列判断正确的是( )
A.两圆锥曲线的离心率分别为![]() ,则“
,则“![]() ”是“两圆锥曲线均为椭圆”的充要条件.
”是“两圆锥曲线均为椭圆”的充要条件.
B.已知![]() 为圆
为圆![]() 内异于圆心的一点,则直线
内异于圆心的一点,则直线![]() 与该圆相交.
与该圆相交.
C.设![]() 是实数,若方程
是实数,若方程![]() 表示双曲线,则
表示双曲线,则![]() .
.
D.命题![]() 的否定是
的否定是![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题:
①函数![]() 的最大值为1;
的最大值为1;
②“若![]() ,则
,则![]() ”的逆命题为真命题;
”的逆命题为真命题;
③若![]() 为锐角三角形,则有
为锐角三角形,则有![]() ;
;
④“![]() ”是“函数
”是“函数![]() 在区间
在区间![]() 内单调递增”的充分必要条件.
内单调递增”的充分必要条件.
其中所有正确命题的序号为____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 图像上一点
图像上一点![]() 处的切线方程为
处的切线方程为![]()
(1)求![]() 的值;
的值;
(2)若方程![]() 在区间
在区间![]() 内有两个不等实根,求
内有两个不等实根,求![]() 的取值范围;
的取值范围;
(3)令![]() 如果
如果![]() 的图像与
的图像与![]() 轴交于
轴交于![]() 两点,
两点,![]() 的中点为
的中点为![]() ,求证:
,求证:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)若点![]() 到直线
到直线![]() 的距离比它到点
的距离比它到点![]() 的距离小
的距离小![]() ,求点
,求点![]() 的轨迹方程.
的轨迹方程.
(2)设椭圆![]() 的离心率为
的离心率为![]() ,焦点在
,焦点在![]() 轴上且长轴长为
轴上且长轴长为![]() ,若曲线
,若曲线![]() 上的点到椭圆
上的点到椭圆![]() 的两个焦点的距离的差绝对值等于
的两个焦点的距离的差绝对值等于![]() ,求曲线
,求曲线![]() 的标准方程.
的标准方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,过底面是矩形的四棱锥FABCD的顶点F作EF∥AB,使AB=2EF,且平面ABFE⊥平面ABCD,若点G在CD上且满足DG=G![]() .
.

求证:(1)FG∥平面AED;
(2)平面DAF⊥平面BAF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com