

 ;(2)O点左侧且距O点1.5 cm处.
;(2)O点左侧且距O点1.5 cm处. 的物理模型为简谐运动.,因此可设所求函数解析式为
的物理模型为简谐运动.,因此可设所求函数解析式为 ,根据
,根据 分别表示简谐运动的振幅,周期,初相的物理意义,与条件中描述的振幅为3cm,周期为3s以及距平衡位置最远处开始计时可求得
分别表示简谐运动的振幅,周期,初相的物理意义,与条件中描述的振幅为3cm,周期为3s以及距平衡位置最远处开始计时可求得 ,从而得到函数表达式为
,从而得到函数表达式为 ;(2)在(1)中求得的函数表达式中令t=5,可得x=-1.5,即可求得物体在t=5s时的位置.
;(2)在(1)中求得的函数表达式中令t=5,可得x=-1.5,即可求得物体在t=5s时的位置. ,
, ,得
,得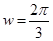 .
. ,∴
,∴ ,又∵
,又∵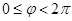 ,∴
,∴ ,从而所求的函数关系式是
,从而所求的函数关系式是 ;
; ,故该物体在t=5 s时的位置是在O点左侧且距O点1.5 cm处..
,故该物体在t=5 s时的位置是在O点左侧且距O点1.5 cm处..  的物理模型简谐运动.
的物理模型简谐运动.

科目:高中数学 来源:不详 题型:单选题
| 3 |
A.
| B.
| C.
| D.
|
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
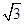 ,b=5,则c的值为________.
,b=5,则c的值为________.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
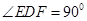 ,
,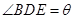 ,
,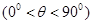 .
.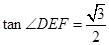 时,求
时,求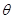 的大小;
的大小;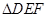 的面积S的最小值及使得S取最小值时
的面积S的最小值及使得S取最小值时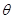 的值.
的值.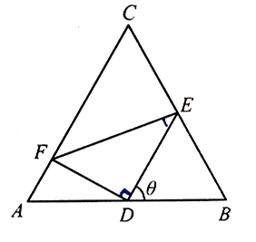
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.北偏东100 | B.北偏西100 | C.南偏东100 | D.南偏西100 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com