
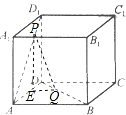
【题目】如图,正方体ABCD﹣A1B1C1D1棱长为1,P、Q分别是线段AD1和BD上的点,且D1P:PA=DQ:QB=5:12, 
(1)求线段PQ的长度;
(2)求证PQ⊥AD;
(3)求证:PQ∥平面CDD1C1 .
【答案】
(1)解:在AD上取点E,使得DE:EA=5:12,
∵D1P:PA=DQ:QB=5:12,
∴PE∥DD1,EQ∥AB,
∴PE⊥AD,EQ⊥AD
∵正方体ABCD﹣A1B1C1D1棱长为1,
∴PE= ![]() ,EQ=
,EQ= ![]() ,
,
∴PQ= ![]() =
= ![]()
(2)证明:∵PE⊥AD,EQ⊥AD,PE∩EQ=E,
∴AD⊥平面PEQ,
∵PQ平面PEQ,
∴PQ⊥AD
(3)证明:∵PE∥DD1,PE平面CDD1C1,DD1平面CDD1C1,
∴PE∥平面CDD1C1,
同理EQ∥平面CDD1C1,
∵PE∩EQ=E,
∴平面PEQ∥平面CDD1C1,
∵PQ平面PEQ,
∴PQ∥平面CDD1C1.
【解析】(1)在AD上取点E,使得DE:EA=5:12,可得PE= ![]() ,ED=
,ED= ![]() ,利用勾股定理,求出线段PQ的长度;(2)证明AD⊥平面PEQ,可得PQ⊥AD;(3)证明平面PEQ∥平面CDD1C1 , 可得PQ∥平面CDD1C1 .
,利用勾股定理,求出线段PQ的长度;(2)证明AD⊥平面PEQ,可得PQ⊥AD;(3)证明平面PEQ∥平面CDD1C1 , 可得PQ∥平面CDD1C1 .
【考点精析】解答此题的关键在于理解棱柱的结构特征的相关知识,掌握两底面是对应边平行的全等多边形;侧面、对角面都是平行四边形;侧棱平行且相等;平行于底面的截面是与底面全等的多边形,以及对空间中直线与直线之间的位置关系的理解,了解相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点.


科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .
.
(1)判断并证明函数f(x)的奇偶性
(2)判断并证明当x∈(﹣1,1)时函数f(x)的单调性;
(3)在(2)成立的条件下,解不等式f(2x﹣1)+f(x)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,图象(折线OEFPMN)描述了某汽车在行驶过程中速度与时间的函数关系,下列说法中错误的是( ) 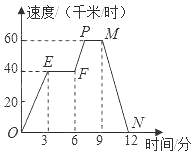
A.第3分时汽车的速度是40千米/时
B.第12分时汽车的速度是0千米/时
C.从第3分到第6分,汽车行驶了120千米
D.从第9分到第12分,汽车的速度从60千米/时减少到0千米/时
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将5个小球放到3个盒子中,在下列条件下,各有多少种投放方法?
①小球不同,盒子不同,盒子不空;
②小球不同,盒子不同,盒子可空;
③小球不同,盒子相同,盒子不空;
④小球不同,盒子相同,盒子可空;
⑤小球相同,盒子不同,盒子不空;
⑥小球相同,盒子不同,盒子可空;
⑦小球相同,盒子相同,盒子不空;
⑧小球相同,盒子相同.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知极坐标系的极点与直角坐标系的原点重合,极轴与![]() 轴的正半轴重合,圆
轴的正半轴重合,圆![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为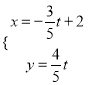 (
(![]() 为参数).
为参数).
(Ⅰ)若![]() ,
, ![]() 是直线
是直线![]() 与
与![]() 轴的交点,
轴的交点, ![]() 是圆
是圆![]() 上一动点,求
上一动点,求![]() 的最大值;
的最大值;
(Ⅱ)若直线![]() 被圆
被圆![]() 截得的弦长等于圆
截得的弦长等于圆![]() 的半径
的半径![]() 倍,求
倍,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com