
分析 (Ⅰ)由已知列关于a,b,c的方程组,求解方程组得到a,b的值,则椭圆方程可求;
(Ⅱ)联立直线方程和椭圆方程,化为关于x的一元二次方程,设出两交点A,B的坐标,利用根与系数关系写出两交点横坐标的和与积,由以AB为直径的圆过椭圆C的右顶点得到$\overrightarrow{AM}•\overrightarrow{BM}$=0,代入向量坐标后结合根与系数关系得到k与m的关系,进一步由直线l过定点,并求出该定点的坐标.
解答 (Ⅰ)解:由题意,$\left\{\begin{array}{l}{e=\frac{c}{a}=\frac{1}{2}}\\{\frac{|\sqrt{6}|}{\sqrt{2}}=b}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得$\left\{\begin{array}{l}{{a}^{2}=4}\\{{b}^{2}=3}\end{array}\right.$.
∴椭圆C的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(Ⅱ)证明:设A(x1,y1),B(x2,y2),
知椭圆C的右顶点为M(2,0),
由$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,得(3+4k2)x2+8mkx+4(m2-3)=0,
且△=3+4k2-m2,
${x}_{1}+{x}_{2}=\frac{-8km}{3+4{k}^{2}}$,${x}_{1}{x}_{2}=\frac{4({m}^{2}-3)}{3+4{k}^{2}}$.
而AM⊥BM,即$\overrightarrow{AM}•\overrightarrow{BM}=0$,
∴(x1-2,y1)•(x2-2,y2)=0,得$(1+{k}^{2}){x}_{1}{x}_{2}+(km-2)({x}_{1}+{x}_{2})+{m}^{2}+4=0$,
∴(1+k2)•$\frac{4({m}^{2}-3)}{3+4{k}^{2}}$-(mk-2)•$\frac{8km}{3+4{k}^{2}}$+m2+4=0,
整理得7m2+16mk+4k2=0,即(m+2k)(7m+2k)=0,
当m=-2k时,l:y=k(x-2)过定点(2,0)为右顶点,与已知矛盾;
当m=-$\frac{2}{7}$k时,l:y=k(x-$\frac{2}{7}$)过定点($\frac{2}{7}$,0),此时△=3+4k2-m2>0;
综上知,直线l过定点($\frac{2}{7}$,0).
点评 本题考查了椭圆的标准方程的求法,考查了直线与圆锥曲线的位置关系,训练了设而不求的解题思想方法和数学转化思想方法,训练了利用向量数量积判断两个向量的垂直关系,是高考试卷中的压轴题.


科目:高中数学 来源: 题型:解答题
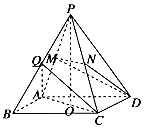 如图,正四棱锥P-ABCD各棱长都为2,点O,M,N,Q分别是AC,PA,PC,PB的中点.
如图,正四棱锥P-ABCD各棱长都为2,点O,M,N,Q分别是AC,PA,PC,PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{π}{4}$,0) | B. | ($\frac{π}{8}$,0) | C. | ($\frac{π}{2}$,0) | D. | ($\frac{5π}{24}$,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\sqrt{5}$ | B. | -$\frac{3}{2}$ | C. | -$\sqrt{2}$ | D. | -$\frac{\sqrt{5}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | k<-1 | B. | k≤-1 | C. | k>2 | D. | k≥2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com