
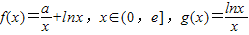 ,其中e是无理数,a∈R.
,其中e是无理数,a∈R.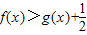 ;
; ,对其求导,求出h(x)的最小值大于0,就可以了.
,对其求导,求出h(x)的最小值大于0,就可以了.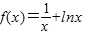 ,∴
,∴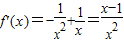 ,(1分)
,(1分)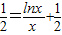 ,x∈(0,e]∴
,x∈(0,e]∴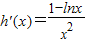 ,(6分)
,(6分)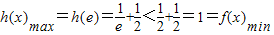 ,
, ,(8分)
,(8分)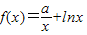 ,(x∈(0,e])有最小值-1,
,(x∈(0,e])有最小值-1,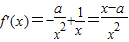 ,(9分)
,(9分)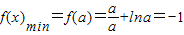 ,,得
,,得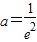 ,满足条件.(12分)
,满足条件.(12分) (舍去),所以,此时无解.(13分)
(舍去),所以,此时无解.(13分)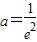 ,使得当x∈(0,e]时f(x)的最小值是-1.(14分)
,使得当x∈(0,e]时f(x)的最小值是-1.(14分) ,x∈(0,e])的最小值是-1,
,x∈(0,e])的最小值是-1,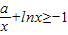 ,对x∈(0,e]恒成立,求“等号”取得时实数a的值.
,对x∈(0,e]恒成立,求“等号”取得时实数a的值.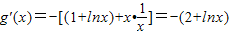 (11分)
(11分)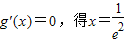
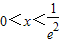 ,g'(x)>0,则g(x)在
,g'(x)>0,则g(x)在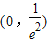 单调递增;
单调递增;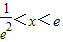 ,g'(x)<0,则g(x)在
,g'(x)<0,则g(x)在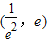 单调递减,(13分)
单调递减,(13分)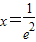 时,g(x)取得最大值,其值是
时,g(x)取得最大值,其值是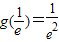
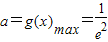 .
.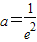 ,使得当x∈(0,e]时f(x)的最小值是-1.(14分)
,使得当x∈(0,e]时f(x)的最小值是-1.(14分)

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源:2012-2013学年山西省忻州一中高三(上)第一次月考数学试卷(理科)(解析版) 题型:解答题
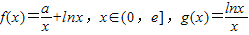 ,其中e是无理数,a∈R.
,其中e是无理数,a∈R.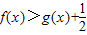 ;
;查看答案和解析>>
科目:高中数学 来源:2012-2013学年山西省忻州一中高三(上)第一次月考数学试卷(理科)(解析版) 题型:解答题
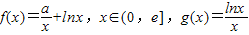 ,其中e是无理数,a∈R.
,其中e是无理数,a∈R.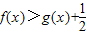 ;
;查看答案和解析>>
科目:高中数学 来源:2009-2010学年数学寒假作业(09)(解析版) 题型:解答题
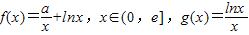 ,其中e是无理数,a∈R.
,其中e是无理数,a∈R.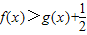 ;
;查看答案和解析>>
科目:高中数学 来源:2010年江苏省南通市高考数学信息试卷(三)(解析版) 题型:解答题
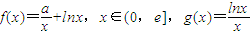 ,其中e是无理数,a∈R.
,其中e是无理数,a∈R.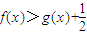 ;
;查看答案和解析>>
科目:高中数学 来源:2010年四川省内江市、广安市高考数学二模试卷(理科)(解析版) 题型:解答题
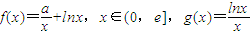 ,其中e是无理数,a∈R.
,其中e是无理数,a∈R.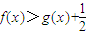 ;
;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com