
(08年绵阳市诊断三理)(12分)![]() 为坐标原点,
为坐标原点,![]() 和
和![]() 两点分别在射线
两点分别在射线![]()
![]() ≥
≥![]() 上移动,且
上移动,且![]() ,动点
,动点![]() 满足
满足![]() ,记点
,记点![]() 的轨迹为
的轨迹为![]() 。
。
(1)求![]() 的值;
的值;
(2)求![]() 点的轨迹
点的轨迹![]() 的方程,并说明它表示怎样的曲线?
的方程,并说明它表示怎样的曲线?
(3)设点![]() ,若直线
,若直线![]()
![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点,且
两点,且![]() 、
、![]() 两点都在以
两点都在以![]() 为圆心的圆上,求
为圆心的圆上,求![]() 的取值范围。
的取值范围。
解析:(1)![]() 分别在射线
分别在射线![]() 上,
上,
![]() ,即
,即![]() ,
,
![]() ,
,
又![]() ,
,
![]() 。
。
![]() ,
,
![]() 。……2分
。……2分
(2)设P(x,y),
由![]() 可得
可得![]()
即![]()
![]() ,
,
两式相减有:![]() ,即
,即![]() 。……6分
。……6分
![]() ,且yA、yB不同时为0,
,且yA、yB不同时为0,
![]() 。
。
∴轨迹C的方程为![]() ,它表示双曲线
,它表示双曲线![]() 的上支。……5分
的上支。……5分
(3)
消去x,整理得:![]() 。……6分
。……6分
∵直线y=kx+m与曲线C交于M,N两点,设M(x1,y1),N(x2,y2),
![]() ,
,
即 ……8分
……8分
由①整理得:m2+3k2-1>0, ④
由③有:3k2-1<0 ⑤
∴由②有m>0。
又![]() 、N在以点G为圆心的圆上,
、N在以点G为圆心的圆上,
设MN的中点为Q,则![]() ,即
,即![]()
![]()
![]() ,
,
![]() 。
。
![]()
![]()
![]() ,
,
![]() 。
。
又![]() ,
,
![]() 。
。
整理得4mk=3k2-1,⑥……10分
把⑥代入④中有:m2+4mk>0,
由m>0,所以m+4k>0,
又由⑥有![]() ,代入上式得
,代入上式得![]() ,
,
![]() ,
,
![]() 中
中![]() 。
。
于是19k2-1<0。
解得![]() 。
。
再由3k2-1<0,得![]() 。
。
综合得k的取值范围为![]() 。……12分
。……12分


科目:高中数学 来源: 题型:
(08年绵阳市诊断三文) 已知函数![]() 图象上斜率为3的两条切线间的距离为
图象上斜率为3的两条切线间的距离为![]() ,f(x)的导数为
,f(x)的导数为![]() ,函数
,函数![]() 。
。
(1)若函数g(x)在x=1有极值,求g(x)的解析式;
(2)若函数g(x)在[-1,1]是增函数,且![]() 在[-1,1]上都成立,求实数m的取值范围。
在[-1,1]上都成立,求实数m的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年绵阳市诊断三理) (12分)某社区举办北京奥运知识宣传活动,现场的“抽卡有奖游戏”特别引人注目,游戏规则是:盒子中装有8张形状大小相同的精美卡片,卡片上分别印有“奥运福娃”或“奥运会徽”,要求4人中一组参加游戏,参加游戏的4人从盒子中轮流抽取卡片,一次抽2张,抽取后不放回,直到4人中一人一次抽到2张“奥运福娃” 卡才能得到奖并终止游戏。
(1)游戏开始之前,一位高中生问:盒子中有几张“奥运会徽” 卡?主持人说:若从盒中任抽2张卡片不都是“奥运会徽” 卡的概率为![]() ,请你回答有几张“奥运会徽” 卡呢?
,请你回答有几张“奥运会徽” 卡呢?
(2)现有甲、乙、丙、丁4人参加游戏,约定甲、乙、丙、丁依次抽取。用![]() 表示4人中的某人获奖终止游戏时总共抽取卡片的次数,求
表示4人中的某人获奖终止游戏时总共抽取卡片的次数,求![]() 的概率分布及
的概率分布及![]() 的数学期望。
的数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:
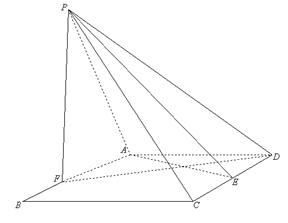
(08年绵阳市诊断三理)(12分)如图,![]() 直二面角中,四边形
直二面角中,四边形![]() 是
是![]() 的菱形,
的菱形,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,设
的中点,设![]() 与平面
与平面![]() 所成的角为
所成的角为![]() 。
。
(1)求证:平面![]() 平面
平面![]() ;
;
(2)试问在线段![]() (不包括端点)上是否存在一点
(不包括端点)上是否存在一点![]() ,使得二面角
,使得二面角![]() 的大小为
的大小为![]() ?若存在,请求出
?若存在,请求出![]() 的长,若不存大,请说明理由。
的长,若不存大,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年绵阳市诊断三理) (12分)若函数![]() 的图象与直线
的图象与直线![]() 相切,并且相邻两个切点的距离为
相切,并且相邻两个切点的距离为![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)将![]() 的图象向右平移
的图象向右平移![]() 个单位后,所得的图象
个单位后,所得的图象![]() 对应的函数
对应的函数![]() 恰好是偶函数,求最小正数
恰好是偶函数,求最小正数![]() ,并求
,并求![]() 的单调递增区间.
的单调递增区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com