
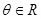 ,
, ,
, 是虚数单位,复数
是虚数单位,复数 ,观察:
,观察: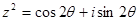 ,
,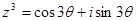 ,…,得出一般性结论为:
,…,得出一般性结论为: _ _______.
_ _______.科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A. 为定点,动点 为定点,动点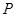 满足 满足 ,则动点 ,则动点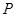 的轨迹是以 的轨迹是以 为焦点的双曲线; 为焦点的双曲线; |
B.由 求出 求出 猜想出数列 猜想出数列 的前 的前 项和 项和 的表达式; 的表达式; |
C.由圆 的面积 的面积 ,猜想出椭圆 ,猜想出椭圆 的面积 的面积 ; ; |
| D.科学家利用鱼的沉浮原理制造潜水艇. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.②①③ | B.③①② | C.①②③ | D.②③① |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 的两边AB、AC互相垂直,则
的两边AB、AC互相垂直,则 。”拓展到空间,类比平面几何的勾股定理,研究三棱锥的侧面积与底面积间的关系,可以得到的正确结论是:“设三棱锥A-BCD的三个侧面ABC 、ACD、ADB两两互相垂直,则 ”。
。”拓展到空间,类比平面几何的勾股定理,研究三棱锥的侧面积与底面积间的关系,可以得到的正确结论是:“设三棱锥A-BCD的三个侧面ABC 、ACD、ADB两两互相垂直,则 ”。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 的边长为1,点
的边长为1,点 在边
在边 上,点
上,点 在边
在边 上,
上, ,动点
,动点 从
从 出发沿直线向
出发沿直线向 运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当点
运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当点 第一次碰到
第一次碰到 时,
时, 与正方形的边碰撞的次数为( )
与正方形的边碰撞的次数为( )| A.16 | B.14 | C.12 | D.10 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com