
设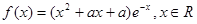 .
.
(Ⅰ)确定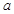 的值,使
的值,使 的极小值为0;
的极小值为0;
(II)证明:当且仅当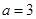 时,
时, 的极大值为3.
的极大值为3.
(Ⅰ)由于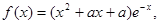 所以
所以
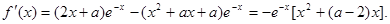 …2分
…2分
令 ,
,
当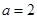 时,
时,
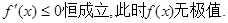 ………3分
………3分
所以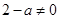 ,
,
当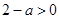 ,即
,即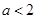 时,
时,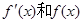 的变化情况如下表1:
的变化情况如下表1:
|
x |
|
0 |
(0, |
|
( |
|
|
- |
0 |
+ |
0 |
- |
|
|
↘ |
极小值 |
↗ |
极大值 |
↘ |
此时应有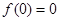 ,所以
,所以 ;………5分
;………5分
②当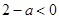 ,即
,即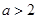 时,
时,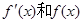 的变化情况如下表2:
的变化情况如下表2:
|
x |
|
|
( |
0 |
(0,+∞) |
|
|
- |
0 |
+ |
0 |
- |
|
|
↘ |
极小值 |
↗ |
极大值 |
↘ |
此时应有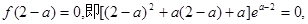
而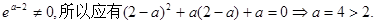
综上可知,当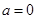 或4时,
或4时,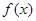 的极小值为
的极小值为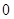 . …………7分
. …………7分
(II)若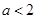 ,则由表1可知,应有
,则由表1可知,应有 也就是
也就是
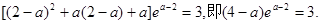 ………9分
………9分
设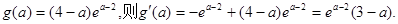
由于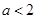 得
得

所以方程 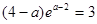 无解.
………11分
无解.
………11分
若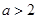 ,则由表2可知,应有
,则由表2可知,应有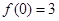 ,即
,即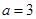 .
.
综上可知,当且仅当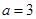 时,
时,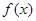 的极大值为
的极大值为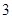 . ………13分
. ………13分
【解析】略


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| nπ |
| 2 |
| nπ |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年山东省兖州市高三第三次模拟考试理科数学卷 题型:解答题
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD//BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M为PC上一点,PA=PD=2,BC=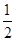 AD=1,CD=
AD=1,CD=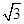 .
.
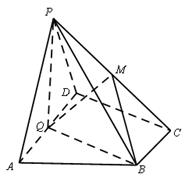
(Ⅰ)求证:平面PQB⊥平面PAD;
(Ⅱ)若二面角M-BQ-C为30°,设PM= MC,试确定
MC,试确定 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)
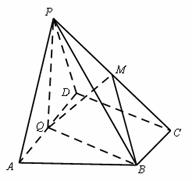 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD//BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M为PC上一点,PA=PD=2,BC=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD//BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M为PC上一点,PA=PD=2,BC=![]() AD=1,CD=
AD=1,CD=![]() .
.
(Ⅰ)求证:平面PQB⊥平面PAD;
(Ⅱ)若二面角M-BQ-C为30°,设PM=![]() MC,试确定
MC,试确定![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com