
【题目】已知等比数列{an}满足an+1+an=104n﹣1(n∈N*),数列{bn}的前n项和为Sn , 且bn=log2an .
(1)求bn , Sn;
(2)设cn= ![]() ,证明:
,证明: ![]() +
+ ![]() +…+
+…+ ![]() <
< ![]() Sn+1(n∈N*).
Sn+1(n∈N*).
【答案】
(1)解:设等比数列{an}的公比为q,
由an+1+an=104n﹣1(n∈N*),可得a1(1+q)qn﹣1=104n﹣1,
即有q=4,a1(1+q)=10,解得a1=2,
则an=24n﹣1=22n﹣1,bn=log2an=log222n﹣1=2n﹣1,
Sn= ![]() (1+2n﹣1)n=n2;
(1+2n﹣1)n=n2;
(2)证明:cn= ![]() =n,
=n,
不等式 ![]() +
+ ![]() +…+
+…+ ![]() <
< ![]() Sn+1,
Sn+1,
即为 ![]() +
+ ![]() +…+
+…+ ![]() <
< ![]() (n+1)2.
(n+1)2.
运用数学归纳法证明.
当n=1时,左边= ![]() ,右边=
,右边= ![]() ×4=2,不等式成立;
×4=2,不等式成立;
假设n=k时,不等式 ![]() +
+ ![]() +…+
+…+ ![]() <
< ![]() (k+1)2.
(k+1)2.
当n=k+1时, ![]() +
+ ![]() +…+
+…+ ![]() +
+ ![]()
< ![]() (k+1)2+
(k+1)2+ ![]() ,
,
要证 ![]() (k+1)2+
(k+1)2+ ![]() <
< ![]() (k+2)2.
(k+2)2.
即证 ![]() <
< ![]() (k+2)2﹣
(k+2)2﹣ ![]() (k+1)2=
(k+1)2= ![]() (2k+3),
(2k+3),
平方可得k2+3k+2<k2+3k+ ![]() ,即有2<
,即有2< ![]() 成立.
成立.
可得n=k+1时,不等式也成立.
综上可得, ![]() +
+ ![]() +…+
+…+ ![]() <
< ![]() Sn+1(n∈N*)
Sn+1(n∈N*)
【解析】(1)设等比数列{an}的公比为q,运用等比数列的通项公式,可得首项为2,公比为4,可得an=22n﹣1 , 由对数的运算性质可得bn=2n﹣1,运用等差数列的求和公式即可得到Sn;(2)求得cn= ![]() =n,原不等式即为
=n,原不等式即为 ![]() +
+ ![]() +…+
+…+ ![]() <
< ![]() (n+1)2 . 运用数学归纳法证明.结合分析法,注意运用假设,化简整理,即可得证.
(n+1)2 . 运用数学归纳法证明.结合分析法,注意运用假设,化简整理,即可得证.
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识,掌握数列{an}的前n项和sn与通项an的关系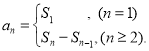 .
.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:高中数学 来源: 题型:
【题目】从一堆产品![]() 正品与次品都多于2件
正品与次品都多于2件![]() 中任取2件,观察正品件数和次品件数,则下列说法:
中任取2件,观察正品件数和次品件数,则下列说法:
![]() “恰好有1件次品”和“恰好2件都是次品”是互斥事件
“恰好有1件次品”和“恰好2件都是次品”是互斥事件
![]() “至少有1件正品”和“全是次品”是对立事件
“至少有1件正品”和“全是次品”是对立事件
![]() “至少有1件正品”和“至少有1件次品”是互斥事件但不是对立事件
“至少有1件正品”和“至少有1件次品”是互斥事件但不是对立事件
![]() “至少有1件次品”和“全是正品”是互斥事件也是对立事件
“至少有1件次品”和“全是正品”是互斥事件也是对立事件
其中正确的有______![]() 填序号
填序号![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)的部分图象如图所示. 
(1)求f(x)的解析式,并求函数f(x)在[﹣ ![]() ,
, ![]() ]上的值域;
]上的值域;
(2)在△ABC中,AB=3,AC=2,f(A)=1,求sin2B.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为{x|x≠0}的偶函数f(x),其导函数为f′(x),对任意正实数x满足xf′(x)>﹣2f(x),若g(x)=x2f(x),则不等式g(x)<g(1﹣x)的解集是( )
A.( ![]() ,+∞)
,+∞)
B.(﹣∞, ![]() )
)
C.(﹣∞,0)∪(0, ![]() )
)
D.(0, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在三棱柱ABCA1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点,
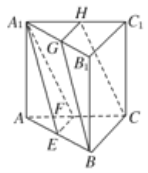
求证:(1)GH∥面ABC
(2)平面EFA1∥平面BCHG.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com