
【题目】某加工厂需定期购买原材料,已知每公斤原材料的价格为1.5元,每次购买原材料需支付运费600元,每公斤原材料每天的保管费用为0.03元,该厂每天需要消耗原材料400公斤,每次购买的原材料当天即开始使用(即有400公斤不需要保管).
(Ⅰ)设该厂每x天购买一次原材料,试写出每次购买的原材料在x天内总的保管费用y1关于x的函数关系式;
(Ⅱ)求该厂多少天购买一次原材料才能使平均每天支付的总费用y最少,并求出这个最少(小)值;
【答案】(Ⅰ)y=6x2-6x(x∈N*,x>1) (Ⅱ)当10天购买一次,最少费用为714元.
【解析】
试题分析:(1)由题知每次购买的原材料在x天内总的保管费用y1=每公斤每天的保管费用×每天需要消耗原材料×使用的天数可得函数关系式;(2)由(1)表示出购买一次原材料的总的费用,利用基本不等式求出y的最小值及此时的x的值即可
试题解析:(1)∵第一天的保管费a1=(400x-400)×0.03=12x-12;
第二天的保管费a2=12x-24,……,组成一个公差为-12的等差数列,
其中项数为:x-1项,(x∈N*,x>1).
∴y1=(x-1)×12(x-1)+![]() =6x2-6x(x∈N*,x>1)
=6x2-6x(x∈N*,x>1)
(2)y=![]() ·(y1+600+400x·1.5)=6x+
·(y1+600+400x·1.5)=6x+![]() +594≥120+594=714(元).
+594≥120+594=714(元).
当且仅当6x=![]() ,即x=10(天)时取“=”号,
,即x=10(天)时取“=”号,
∴当10天购买一次,最少费用为714元.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】已知两直线l1:ax﹣by+4=0,l2:(a﹣1)x+y+b=0,分别求满足下列条件的a,b值
(1)l1⊥l2,且直线l1过点(﹣3,﹣1);
(2)l1∥l2,且直线l1在两坐标轴上的截距相等.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知长方形![]() 中,
中,![]() 为
为![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() .
.
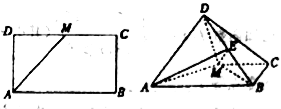
(1)求证:![]() ;
;
(2)若点![]() 是线段
是线段![]() 上的一动点,问点
上的一动点,问点![]() 在何位置时,三棱锥
在何位置时,三棱锥![]() 的体积与四棱锥
的体积与四棱锥![]() 的体积之比为1:3?
的体积之比为1:3?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题中:
①函数![]() 的一个对称中心为
的一个对称中心为![]() ;
;
②若![]() ,
, ![]() 为第一象限角,且
为第一象限角,且![]() ,则
,则![]() ;
;
③若![]() ,则存在实数
,则存在实数![]() ,使得
,使得![]() ;
;
④点![]() 是三角形
是三角形![]() 所在平面内一点,且满足
所在平面内一点,且满足![]() ,则点
,则点![]() 是三角形
是三角形![]() 的内心.
的内心.
其中正确的序号是__________.(把你认为正确的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次测验中,有6位同学的平均成绩为75分, 用xn表示编号为n(n=1,2,…,6)的同学所得成绩,且前5位同学的成绩如下:
编号n | 1 | 2 | 3 | 4 | 5 |
成绩xn | 70 | 76 | 72 | 70 | 72 |
(1)求第6位同学的成绩x6,及这6位同学成绩的标准差s;
(2)从前5位同学中选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以原点
中,以原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程并指出其形状;
的直角坐标方程并指出其形状;
(2)设![]() 是曲线
是曲线![]() 上的动点,求
上的动点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn,且首项a1≠3,an+1=Sn+3n(n∈N*).
(1)求证:数列{Sn-3n}是等比数列;
(2)若{an}为递增数列,求a1的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com