
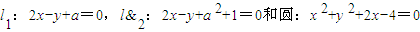 相切,则a的取值范围是( )
相切,则a的取值范围是( )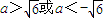
 或
或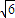 ≤a≤7
≤a≤7科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西稳派名校学术联盟高三12月调研理科数学试卷(解析版) 题型:选择题
对于两条平行直线和圆的位置关系定义如下:若两直线中至少有一条与圆相切,则称该位置关系为“平行相切”;若两直线都与圆相离,则称该位置关系为“平行相离”;否则称为“平行相交”。已知直线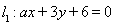 ,
,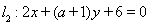 ,和圆C:
,和圆C: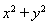
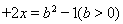 的位置关系是“平行相交”,则b的取值范围为( )
的位置关系是“平行相交”,则b的取值范围为( )
A. 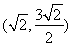 B.
B. 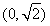
C.  D.
D. 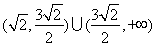
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省高三上学期四调考试文科数学试卷(解析版) 题型:选择题
两条平行直线和圆的位置关系定义为:若两条平行直线和圆有四个不同的公共点,则称两条平行线和圆“相交”;若两平行直线和圆没有公共点,则称两条平行线和圆“相离”;若两平行直线和圆有一个、两个或三个不同的公共点,则称两条平行线和圆“相切”.已知直线 相切,则a的取值范围是( )
相切,则a的取值范围是( )
A. B.
B.
C.-3≤a≤一 或
或 ≤a≤7 D.a≥7或a≤—3
≤a≤7 D.a≥7或a≤—3
查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省漳州市四地七校高三6月模拟考理科数学试卷(解析版) 题型:选择题
两条平行直线和圆的位置关系定义为:若两条平行直线和圆有四个不同的公共点,则称两条平行线和圆“相交”;若两平行直线和圆没有公共点,则称两条平行线和圆“相离”;若两平行直线和圆有一个、两个或三个不同的公共点,则称两条平行线和圆“相切”.已知直线 ,
, 和圆
和圆 相切,则
相切,则 的取值范围是( )
的取值范围是( )
A.
B. 或
或
C.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com