
【题目】在平面直角坐标系xOy中,将曲线方程![]() ,先向左平移2个单位,再向上平移2个单位,得到曲线C.
,先向左平移2个单位,再向上平移2个单位,得到曲线C.
(1)点M(x,y)为曲线C上任意一点,写出曲线C的参数方程,并求出![]() 的最大值;
的最大值;
(2)设直线l的参数方程为![]() ,(t为参数),又直线l与曲线C的交点为E,F,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段EF的中点且与l垂直的直线的极坐标方程.
,(t为参数),又直线l与曲线C的交点为E,F,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段EF的中点且与l垂直的直线的极坐标方程.
【答案】(1)![]() (θ为参数);4;(2)
(θ为参数);4;(2)![]()
【解析】
(1)直接利用转换关系,把参数方程极坐标方程和直角坐标方程之间进行转换,进一步利用三角函数关系式的变换和余弦型函数性质的应用求出结果.
(2)利用中点坐标公式的应用和直线垂直的充要条件的应用求出结果.
解:(1)将曲线方程![]() ,先向左平移2个单位,再向上平移2个单位,得到曲线C的方程为
,先向左平移2个单位,再向上平移2个单位,得到曲线C的方程为![]() ,
,
即![]() ,
,
故曲线C的参数方程为![]() (θ为参数);
(θ为参数);
又点M(x,y)为曲线C上任意一点,
所以![]() 2cos
2cos![]() 4cos(
4cos(![]() ).
).
所以![]() 的最大值为4;
的最大值为4;
(2)由(1)知曲线C的直角坐标方程为![]() ,
,
又直线l的参数方程为![]() ,(t为参数),
,(t为参数),
所以直线l的普通方程为x+2y﹣4=0,
所以有 ,
,
解得![]() 或
或![]() .
.
所以线段EF的中点坐标为(![]() ),
),
即线段EF的中点坐标为(2,1),
直线l的斜率为![]() ,
,
则与直线l垂直的直线的斜率为2,
故所求直线的直角坐标方程为y﹣1=2(x﹣2),
即2x﹣y﹣3=0,
将x=ρcosθ,y=ρsinθ代入,
得其极坐标方程为2ρcosθ﹣ρsinθ﹣3=0.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源: 题型:
【题目】已知正△ABC边长为3,点M,N分别是AB,AC边上的点,AN=BM=1,如图1所示.将△AMN沿MN折起到△PMN的位置,使线段PC长为![]() ,连接PB,如图2所示.
,连接PB,如图2所示.
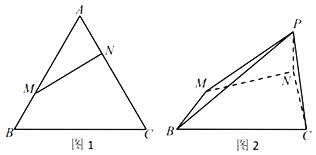
(Ⅰ)求证:平面PMN⊥平面BCNM;
(Ⅱ)若点D在线段BC上,且BD=2DC,求二面角M﹣PD﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱柱![]() ,底面
,底面![]() 为等腰梯形,
为等腰梯形,![]() ;
;![]() ,侧面
,侧面![]() 底面
底面![]() .
.
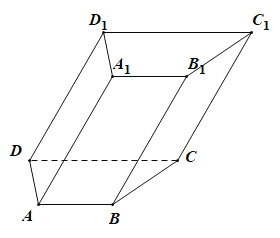
(1)在侧面![]() 中能否作一条直线使其与
中能否作一条直线使其与![]() 平行?如果能,请写出作图过程并给出证明;如果不能,请说明理由;
平行?如果能,请写出作图过程并给出证明;如果不能,请说明理由;
(2)求四面体![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 1(a>b>0),F1,F2为椭圆的左右焦点,过F2的直线交椭圆与A、B两点,∠AF1B=90°,2
1(a>b>0),F1,F2为椭圆的左右焦点,过F2的直线交椭圆与A、B两点,∠AF1B=90°,2![]() ,则椭圆的离心率为( )
,则椭圆的离心率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com