
【题目】我国古代数学名著《九章算术》的论割圆术中有:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣.”它体现了一种无限与有限的转化过程.比如在表达式1+ ![]() 中“”即代表无数次重复,但原式却是个定值,它可以通过方程1+
中“”即代表无数次重复,但原式却是个定值,它可以通过方程1+ ![]() =x求得x=
=x求得x= ![]() .类比上述过程,则
.类比上述过程,则 ![]() =( )
=( )
A.3
B.![]()
C.6
D.2 ![]()
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上且以4为周期的奇函数,当x∈(0,2)时,f(x)=ln(x2﹣x+b),若函数f(x)在区间[﹣2,2]上的零点个数为5,则实数b的取值范围是
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正实数a,b满足:a+b=2.
(1)求 ![]() 的最小值m;
的最小值m;
(2)设函数f(x)=|x﹣t|+|x+ ![]() |(t≠0),对于(Ⅰ)中求得的m,是否存在实数x,使得f(x)=m成立,若存在,求出x的取值范围,若不存在,说明理由.
|(t≠0),对于(Ⅰ)中求得的m,是否存在实数x,使得f(x)=m成立,若存在,求出x的取值范围,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知D,E是△ABC边BC的三等分点,点P在线段DE上,若 ![]() =x
=x ![]() +y
+y ![]() ,则xy的取值范围是( )
,则xy的取值范围是( )
A.[ ![]() ,
, ![]() ]
]
B.[ ![]() ,
, ![]() ]
]
C.[ ![]() ,
, ![]() ]
]
D.[ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在以A,B,C,D,E,F为顶点的多面体中,四边形ACDF是菱形,∠FAC=60°,AB∥DE,BC∥EF,AB=BC=3,AF=2 ![]() .
. 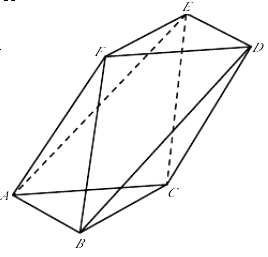
(1)求证:平面ABC⊥平面ACDF;
(2)求平面AEF与平面ACE所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1中,∠B1A1A=∠C1A1A=60°,AA1=AC=4,AB=2,P,Q分别为棱AA1 , AC的中点. 
(1)在平面ABC内过点A作AM∥平面PQB1交BC于点M,并写出作图步骤,但不要求证明;
(2)若侧面ACC1A1⊥侧面ABB1A1 , 求直线A1C1与平面PQB1所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线 ![]() (t为参数)恒过椭圆
(t为参数)恒过椭圆 ![]() (φ为参数)在右焦点F.
(φ为参数)在右焦点F.
(1)求m的值;
(2)设直线l与椭圆C交于A,B两点,求|FA||FB|的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2lnx+x2+(a﹣1)x﹣a,(a∈R),当x≥1时,f(x)≥0恒成立.
(1)求实数a的取值范围;
(2)若正实数x1、x2(x1≠x2)满足f(x1)+f(x2)=0,证明:x1+x2>2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com