
【题目】(理)如图,在正方体ABCD﹣A1B1C1D1中,点O为线段BD的中点.设点P在线段CC1上,直线OP与平面A1BD所成的角为α,则sinα的取值范围是( ) 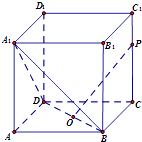
A.[ ![]() ,1]
,1]
B.[ ![]() ,1]
,1]
C.[ ![]() ,
, ![]() ]
]
D.[ ![]() ,1]
,1]
 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:
【题目】等边三角形ABC与正方形ABDE有一公共边AB,二面角C﹣AB﹣D的余弦值为 ![]() ,M,N分别是AC.BC的中点,则EM,AN所成角的余弦值等于( )
,M,N分别是AC.BC的中点,则EM,AN所成角的余弦值等于( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“神州”号飞船返回舱顺利到达地球后,为了及时将航天员救出,地面指挥中心在返回舱预计到达的区域安排了同一条直线上的三个救援中心(记为B,C,D).当返回舱距地面1万米的P点时(假定以后垂直下落,并在A点着陆),C救援中心测得飞船位于其南偏东60°方向,仰角为60°,B救援中心测得飞船位于其南偏西30°方向,仰角为30°.D救援中心测得着陆点A位于其正东方向.
(1)求B,C两救援中心间的距离;
(2)D救援中心与着陆点A间的距离.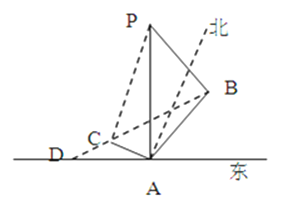
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sinx,将函数y=f(x)的图象向右平移![]() 个单位,再把横坐标缩短到原来的
个单位,再把横坐标缩短到原来的![]() (纵坐标不变),得到函数y=g(x)的图象,求函数y=g(x)的解析式,并写出它的单调递增区间.
(纵坐标不变),得到函数y=g(x)的图象,求函数y=g(x)的解析式,并写出它的单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】10名工人某天生产同一零件,生产的件数是15,17,14,10,15,17,17,16,14,12,设其平均数为a,中位数为b,众数为c,则有( )
A.a>b>c
B.b>c>a
C.c>a>b
D.c>b>a
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,底面ABCD是菱形,∠BAD=60°,AB=2,PD= ![]() ,O为AC与BD的交点,E为棱PB上一点.
,O为AC与BD的交点,E为棱PB上一点.
(Ⅰ)证明:平面EAC⊥平面PBD;
(Ⅱ)若PD∥平面EAC,求三棱锥P﹣EAD的体积.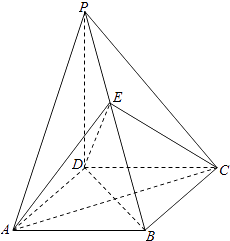
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角梯形PBCD中, ![]() ,A为PD的中点,如图.将△PAB沿AB折到△SAB的位置,使SB⊥BC,点E在SD上,且
,A为PD的中点,如图.将△PAB沿AB折到△SAB的位置,使SB⊥BC,点E在SD上,且 ![]() ,如图.
,如图.
(Ⅰ)求证:SA⊥平面ABCD;
(Ⅱ)求二面角E﹣AC﹣D的正切值.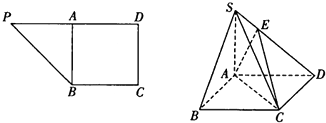
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是等比数列,首项a1=2,a4=16
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{bn}是等差数列,且b3=a3 , b5=a5 , 求数列{bn}的通项公式及前n项的和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=sin(ωx+φ)+cos(ωx+φ) ![]() 的最小正周期为π,且f(﹣x)=f(x),则( )
的最小正周期为π,且f(﹣x)=f(x),则( )
A.f(x)在 ![]() 单调递减
单调递减
B.f(x)在( ![]() ,
, ![]() )单调递减
)单调递减
C.f(x)在(0, ![]() )单调递增
)单调递增
D.f(x)在( ![]() ,
, ![]() )单调递增
)单调递增
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com