
【题目】用一个平行于圆锥底面的平面去截圆锥,截得圆台的母线长为![]() ,两底面面积分别为
,两底面面积分别为![]() 和
和![]() .求:
.求:
(1)圆台的高;
(2)圆台的体积;
(3)截得此圆台的圆锥的表面积.
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源: 题型:
【题目】交通安全法有规定:机动车行经人行横道时,应当减速行驶;遇行人正在通过人行横道,应当停车让行.机动车行经没有交通信号的道路时,遇行人横过马路,应当避让.我们将符合这条规定的称为“礼让斑马线”,不符合这条规定的称为“不礼让斑马线”.下表是六安市某十字路口监控设备所抓拍的5个月内驾驶员“不礼让斑马线”行为的统计数据:
月份 | 1 | 2 | 3 | 4 | 5 |
“不礼让斑马线”的驾驶员人数 | 120 | 105 | 100 | 85 | 90 |
(1)根据表中所给的5个月的数据,可用线性回归模型拟合![]() 与
与![]() 的关系,请用相关系数加以说明;
的关系,请用相关系数加以说明;
(2)求“不礼让斑马线”的驾驶员人数![]() 关于月份
关于月份![]() 之间的线性回归方程;
之间的线性回归方程;
(3)若从4,5月份“不礼让斑马线”的驾驶员中分别选取4人和2人,再从所选取的6人中任意抽取2人进行交规调查,求抽取的2人分别来自两个月份的概率;
参考公式:线性回归方程![]() ,其中
,其中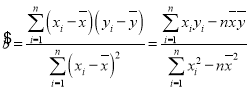 ,
,![]() ,
, .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十九大以来,某贫困地区扶贫办积极贯彻落实国家精准扶贫的政策要求,带领广大农村地区人民群众脱贫奔小康.经过不懈的奋力拼搏,新农村建设取得巨大进步,农民年收入也逐年增加.为了制定提升农民年收入、实现2020年脱贫的工作计划,该地扶贫办统计了2019年50位农民的年收入并制成如下频率分布直方图:

(1)根据频率分布直方图,估计50位农民的年平均收入![]() 元(单位:千元)(同一组数据用该组数据区间的中点值表示);
元(单位:千元)(同一组数据用该组数据区间的中点值表示);
(2)由频率分布直方图,可以认为该贫困地区农民年收入X服从正态分布![]() ,其中
,其中![]() 近似为年平均收入
近似为年平均收入![]() ,
,![]() 近似为样本方差
近似为样本方差![]() ,经计算得
,经计算得![]() ,利用该正态分布,求:
,利用该正态分布,求:
(i)在扶贫攻坚工作中,若使该地区约有占总农民人数的84.14%的农民的年收入高于扶贫办制定的最低年收入标准,则最低年收入大约为多少千元?
(ii)为了调研“精准扶贫,不落一人”的政策要求落实情况,扶贫办随机走访了1000位农民.若每位农民的年收入互相独立,问:这1000位农民中的年收入不少于12.14千元的人数最有可能是多少?
附参考数据:![]() ,若随机变量X服从正态分布
,若随机变量X服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 在
在![]() 处取得极大值或极小值,则称
处取得极大值或极小值,则称![]() 为函数
为函数![]() 的极值点.设函数
的极值点.设函数![]() ,
,![]() ,a,b,k
,a,b,k![]() R.
R.
(1)若![]() 为
为![]() 在x=1处的切线.①当
在x=1处的切线.①当![]() 有两个极值点
有两个极值点![]() ,
,![]() ,且满足
,且满足![]() ·
·![]() =1时,求b的值及a的取值范围;②当函数
=1时,求b的值及a的取值范围;②当函数![]() 与
与![]() 的图象只有一个交点,求a的值;
的图象只有一个交点,求a的值;
(2)若对满足“函数![]() 与
与![]() 的图象总有三个交点P,Q,R”的任意突数k,都有PQ=QR成立,求a,b,k满足的条件.
的图象总有三个交点P,Q,R”的任意突数k,都有PQ=QR成立,求a,b,k满足的条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产某种产品的年固定成本为250万元,每生产![]() 千件,需另投入成本
千件,需另投入成本![]() ,当年产量不足80千件时,
,当年产量不足80千件时,![]() (万元);当年产量不小于80千件时,
(万元);当年产量不小于80千件时,![]() (万元),每件售价为0.05万元,通过市场分析,该厂生产的商品能全部售完.
(万元),每件售价为0.05万元,通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从甲地到乙地要经过3个十字路口,设各路口信号灯工作相互独立,且在各路口遇到红灯的概率分别为![]() .
.
(Ⅰ)设![]() 表示一辆车从甲地到乙地遇到红灯的个数,求随机变量
表示一辆车从甲地到乙地遇到红灯的个数,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)若有2辆车独立地从甲地到乙地,求这2辆车共遇到1个红灯的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】万众瞩目的2018年俄罗斯世界杯决赛于北京时间2018年7月15日23时在俄罗斯莫斯科的卢日尼基体育场进行.为确保总决赛的顺利进行,组委会决定在比赛地点卢日尼基球场外临时围建一个矩形观众候场区,总面积为![]() (如图所示).要求矩形场地的一面利用体育场的外墙,其余三面用铁栏杆围,并且要在体育馆外墙对面留一个长度为
(如图所示).要求矩形场地的一面利用体育场的外墙,其余三面用铁栏杆围,并且要在体育馆外墙对面留一个长度为![]() 的入口.现已知铁栏杆的租用费用为100元/
的入口.现已知铁栏杆的租用费用为100元/![]() .设该矩形区域的长为
.设该矩形区域的长为![]() (单位:
(单位:![]() ),租用铁栏杆的总费用为
),租用铁栏杆的总费用为![]() (单位:元).
(单位:元).

(1)将![]() 表示为
表示为![]() 的函数;
的函数;
(2)试确定![]() ,使得租用此区域所用铁栏杆所需费用最小,并求出最小费用.
,使得租用此区域所用铁栏杆所需费用最小,并求出最小费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com