
(1)y=|x|-1,x∈{-2,-1,0,1,2};(2)y=x2+4x+3,(-3≤x≤1);
(3)y=![]() ;(4)y=2x-3+
;(4)y=2x-3+![]() ;(5)y=
;(5)y=![]() .
.
解析:求函数的值域应确定相应的定义域后再根据函数的具体形式及运算确定其值域.(1)本例解析较简单,故可用“直接法”根据定义域及对应法则得到该函数的值域.(2) 对于二次函数值域的求法,常采用配方法或作出二次函数的图象求得.(3)对于形如y=![]() (a≠0)型函数值域的求法,常借助反比例函数y=
(a≠0)型函数值域的求法,常借助反比例函数y=![]() (k≠0)的值域解决.(4) 没有给定自变量的取值范围,应先考查函数的定义域,再求其值域.对于形如y=ax+b±
(k≠0)的值域解决.(4) 没有给定自变量的取值范围,应先考查函数的定义域,再求其值域.对于形如y=ax+b±![]() (a,b,c,d为常数,且ac≠0)的函数值域的求法,常借用整体思想利用“换元法”求值域.(5) 形如y=
(a,b,c,d为常数,且ac≠0)的函数值域的求法,常借用整体思想利用“换元法”求值域.(5) 形如y=![]() 型的函数,由于任一函数的定义域都不可能是空集,所以可将函数化为:(ya2-a1)x2+(yb2-b1)x+yc2-c1=0.当ya2-a1≠0时,上式是关于x的一元二次方程,因此该方程的根的判别式Δ≥0,根据这个不等式可求出函数的值域,当然ya2-a1=0也要考虑.
型的函数,由于任一函数的定义域都不可能是空集,所以可将函数化为:(ya2-a1)x2+(yb2-b1)x+yc2-c1=0.当ya2-a1≠0时,上式是关于x的一元二次方程,因此该方程的根的判别式Δ≥0,根据这个不等式可求出函数的值域,当然ya2-a1=0也要考虑.
解:(1)∵x∈{-2,-1,0,1,2},y=|x|-1,
∴y∈{-1,0,1}.
(2)法一:∵-3≤x≤1,y=x2+4x+3=(x+2)2-1,
∴y∈{y|-1≤y≤8}.
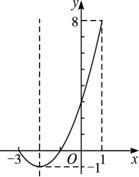
法二:画出y=x2+4x+3,(-3≤x≤1)的图象,
如图所示,当x∈{x|-3≤x≤1}时,得y∈{y|0≤y≤8}.
(3)∵ y=![]() =
=![]() =2+
=2+![]() ,由
,由![]() ≠0,有 y≠2,
≠0,有 y≠2,
∴函数的值域为{y|y∈R,且y≠2}.
(4)∵4x-13≥0,∴x≥![]() .令t=
.令t=![]() ,则得x=
,则得x=![]() .
.
∴y=![]() t2+t+
t2+t+![]() =
=![]() (t+1)2+3,因为x≥
(t+1)2+3,因为x≥![]() ,∴t≥0,因此y≥
,∴t≥0,因此y≥![]() .
.
∴函数 y=2x-3+![]() 的值域为{y|y≥
的值域为{y|y≥![]() }.
}.
(5)由y=![]() 得x∈R,且可化为 (2y-1)x2+2(y+1)x+(y+3)=0,
得x∈R,且可化为 (2y-1)x2+2(y+1)x+(y+3)=0,
∴当 y≠![]() 时,Δ=[2(y+1)]2-4(2y-1)(y+3)≥0.
时,Δ=[2(y+1)]2-4(2y-1)(y+3)≥0.
∴y2+3y-4≤0.∴-4≤y≤1且∴y≠![]() .
.
又当y=![]() 时,代入方程得x=-
时,代入方程得x=-![]() ,满足条件.
,满足条件.
∴函数y=![]() 的值域为{y|-4≤y≤1}.
的值域为{y|-4≤y≤1}.


科目:高中数学 来源: 题型:
| 1+sinx |
| 2+cosx |
| ex-e-x |
| ex+e-x |
| 1 |
| x |
| ||
| x+2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com