
【题目】4月23日是“世界读书日”,某中学在此期间开展了一系列的读书教育活动.为了解高三学生课外阅读情况,采用分层抽样的方法从高三某班甲、乙、丙、丁四个小组中随机抽取10名学生参加问卷调查.各组人数统计如下:

(1)从参加问卷调查的10名学生中随机抽取两名,求这两名学生来自同一个小组的概率;
(2)在参加问卷调查的10名学生中,从来自甲、丙两个小组的学生中随机抽取两名,用![]() 表示抽得甲组学生的人数,求
表示抽得甲组学生的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
科目:高中数学 来源: 题型:
【题目】探究函数![]() ,
,![]() 上的最小值,并确定取得最小值时
上的最小值,并确定取得最小值时![]() 的值,列表如下:
的值,列表如下:
| … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| … | 14 | 7 | 5.34 | 5.11 | 5.01 | 5 | 5.01 | 5.04 | 5.08 | 5.67 | 7 | 8.6 | 12.14 | … |
(1)观察表中![]() 值随
值随![]() 值变化趋势特点,请你直接写出函数
值变化趋势特点,请你直接写出函数![]() ,
,![]() 的单调区间,并指出当
的单调区间,并指出当![]() 取何值时函数的最小值为多少;
取何值时函数的最小值为多少;
(2)用单调性定义证明函数![]() 在
在![]() 上的单调性.
上的单调性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[2018·江西联考]交强险是车主必须为机动车购买的险种,若普通6座以下私家车投保交强险第一年的费用(基准保费)统一为![]() 元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就越高,具体浮动情况如表:
元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就越高,具体浮动情况如表:
交强险浮动因素和浮动费率比率表 | ||
浮动因素 | 浮动比率 | |
| 上一个年度未发生有责任道路交通事故 | 下浮10% |
| 上两个年度未发生有责任道路交通事故 | 下浮20% |
| 上三个及以上年度未发生有责任道路交通事故 | 下浮30% |
| 上一个年度发生一次有责任不涉及死亡的道路交通事故 | 0% |
| 上一个年度发生两次及两次以上有责任道路交通事故 | 上浮10% |
| 上一个年度发生有责任道路交通死亡事故 | 上浮30% |
某机构为了研究某一品牌普通6座以下私家车的投保情况,随机抽取了80辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:
类型 |
|
|
|
|
| |
数量 | 20 | 10 | 10 | 20 | 15 | 5 |
以这80辆该品牌车的投保类型的频率代替一辆车投保类型的概率,完成下列问题:
(1)按照我国《机动车交通事故责任强制保险条例》汽车交强险价格的规定,![]() .某同学家里有一辆该品牌车且车龄刚满三年,记X为该品牌车在第四年续保时的费用,求X的分布列与数学期望值;(数学期望值保留到个位数字)
.某同学家里有一辆该品牌车且车龄刚满三年,记X为该品牌车在第四年续保时的费用,求X的分布列与数学期望值;(数学期望值保留到个位数字)
(2)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车.假设购进一辆事故车亏损4000元,一辆非事故车盈利8000元:
①若该销售商购进三辆(车龄已满三年)该品牌二手车,求这三辆车中至多有一辆事故车的概率;
②若该销售商一次购进100辆(车龄已满三年)该品牌二手车,求他获得利润的期望值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数学老师给出一个函数![]() ,甲、乙、丙、丁四个同学各说出了这个函数的一条性质:甲:在
,甲、乙、丙、丁四个同学各说出了这个函数的一条性质:甲:在![]() 上函数单调递减;乙:在
上函数单调递减;乙:在![]() 上函数单调递增;丙:在定义域R上函数的图象关于直线
上函数单调递增;丙:在定义域R上函数的图象关于直线![]() 对称;丁:
对称;丁:![]() 不是函数的最小值.老师说:你们四个同学中恰好有三个人说的正确.那么,你认为____说的是错误的.
不是函数的最小值.老师说:你们四个同学中恰好有三个人说的正确.那么,你认为____说的是错误的.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设直线l的方程为![]() ,圆O的方程为
,圆O的方程为![]() .
.
(1)当m取一切实数时,直线l与圆O都有公共点,求r的取值范围;
(2)当![]() 时,直线
时,直线![]() 与圆O交于M,N两点,若
与圆O交于M,N两点,若![]() ,求实数t的取值范围.
,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知各项均为正数的无穷数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() (其中
(其中![]() 为常数),
为常数),![]()
![]() .数列
.数列![]() 满足
满足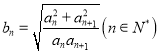 .
.
(1)证明数列![]() 是等差数列,并求出
是等差数列,并求出![]() 的通项公式;
的通项公式;
(2)若无穷等比数列![]() 满足:对任意的
满足:对任意的![]() ,数列
,数列![]() 中总存在两个不同的项
中总存在两个不同的项![]() ,
, ![]()
![]() 使得
使得![]() ,求
,求![]() 的公比
的公比![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
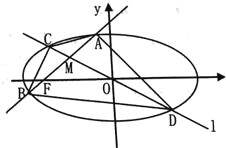
【题目】如图,已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,过左焦点
,过左焦点![]() 且斜率为
且斜率为![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,直线
,直线![]() :
:![]() 交椭圆
交椭圆![]() 于
于![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)求证:点![]() 在直线
在直线![]() 上;
上;
(3)是否存在实数![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com