
���� ��1���������������������㣬�����ݶ����ǵ������ҹ�ʽ�����Ǻ͵����ҹ�ʽ���л��������f��x��=$2sin��2��x+\frac{��}{6}��$���Ӷ��ó�f��x��������Ϊ$\frac{��}{��}$������������ɵó�$\frac{��}{2��}�ݦ�$���Ӷ����$�ء�\frac{1}{2}$��
��2�����ݦ����ʱ��f��2A��=1��ɵõ�$sin��2A+\frac{��}{6}��=\frac{1}{2}$����������0��A���б�ɵó�A=$\frac{��}{3}$��������$\overrightarrow{m}��\overrightarrow{n}$���߱�ɵõ�$sinC=2sinB=2sin��\frac{2��}{3}-C��$������������C=$\frac{��}{2}$����������ֱ�������εı߽ǹ�ϵ�������b��c��
��� �⣺��1��$f��x��=\overrightarrow{m}•\overrightarrow{n}=co{s}^{2}��x-si{n}^{2}��x$$+2\sqrt{3}sin��xcos��x$=$cos2��x+\sqrt{3}sin2��x$=$2sin��2��x+\frac{��}{6}��$��
��f��x��������Ϊ$\frac{��}{��}$��
f��x����ͼ�������������Գ����ĵľ�����ڵ��ڦУ�
��$\frac{��}{2��}�ݦ�$��
��$�ء�\frac{1}{2}$��
��ص�ȡֵ��ΧΪ$��-�ޣ�\frac{1}{2}]$��
��2�������Ϊ$\frac{1}{2}$����ʱf��x��=$2sin��x+\frac{��}{6}��$��
��$f��2A��=2sin��2A+\frac{��}{6}��=1$��
��$sin��2A+\frac{��}{6}��=\frac{1}{2}$��
��0��A����
��$\frac{��}{6}��2A+\frac{��}{6}��\frac{13��}{6}$��
��$2A+\frac{��}{6}=\frac{5��}{6}$��
��$A=\frac{��}{3}$��
��$\overrightarrow{m}$��$\overrightarrow{n}$���ߣ�
��sinC-2sinB=0��
��sinC=2sinB��
��$sinC=2sin��\frac{2��}{3}-C��$=$2sin\frac{2��}{3}cosC-2cos\frac{2��}{3}sinC$=$\sqrt{3}cosC+sinC$��
��cosC=0��C=$\frac{��}{2}$��
��$c=\frac{a}{sinA}=\frac{\sqrt{3}}{\frac{\sqrt{3}}{2}}=2$��b=ccosA=2cos$\frac{��}{3}$=1��
���� �����������������������㣬�����ǵ������ҹ�ʽ�����Ǻ͵����ҹ�ʽ���Լ�����y=Asin����x+�գ��ĺ��������ڹ�ʽ���Գ����ģ������ε��ڽǺ�Ϊ�У����������������ϵ���Լ�ֱ�������εı߽ǹ�ϵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
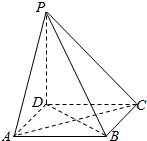 ��ͼ������P-ABCD�ĸ��ⳤ��Ϊa��
��ͼ������P-ABCD�ĸ��ⳤ��Ϊa���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com