
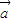 ,
,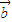 满足|
满足|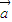 |=2|
|=2| |≠0,且关于x的函数f(x)=2x3+3|
|≠0,且关于x的函数f(x)=2x3+3|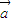 |x2+6
|x2+6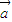 •
•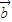 x+5 在实数集R上单调递增,则向量
x+5 在实数集R上单调递增,则向量 ,
,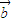 的夹角的取值范围是( )
的夹角的取值范围是( )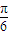 ]
]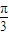 ]
]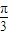 ]
]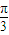 ,π]
,π]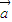 |=2|
|=2|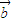 |≠0,利用向量的数量积,即可得到结论.
|≠0,利用向量的数量积,即可得到结论.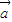 |x+6
|x+6 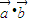 ,则由函数f(x)=2x3+3|a|x2+6a•bx+5 在实数集R上单调递增,
,则由函数f(x)=2x3+3|a|x2+6a•bx+5 在实数集R上单调递增,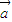 |x+6
|x+6 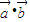 ≥0恒成立,即 x2+|
≥0恒成立,即 x2+|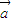 |x+
|x+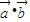 ≥0恒成立,故判别式△=
≥0恒成立,故判别式△=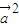 -4
-4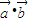 ≤0 恒成立,
≤0 恒成立,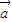 |=2|
|=2|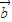 |≠0,可得 4
|≠0,可得 4 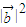 ≤8|
≤8|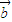 |•|
|•|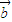 |cos<
|cos<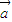 ,
, >,
>,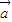 ,
,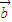 >≥
>≥ ,
,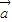 ,
,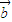 >∈[0,
>∈[0,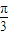 ],
],

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com