
【题目】设函数![]() .
.
(1)若不等式![]() 的解集为
的解集为![]() ,求实数
,求实数![]() 、
、![]() 的值;
的值;
(2)解不等式![]() .
.
【答案】(1) 
(2) ![]() 时解集为
时解集为![]() ,
,![]() 时解集为
时解集为![]() ,
,![]() 时解集为
时解集为![]() ,
,![]() 时解集为
时解集为![]() ,
,![]() 时解集为
时解集为![]()
【解析】
试题分析:(1)根据一元二次不等式的解集,利用根与系数的关系,即可求出实数a、m的值;
(2)不等式化为(ax-1)(x-1)<0,讨论a=0和a>0、a<0时,求出不等式f(x)<0的解集即可
试题解析:⑴∵![]() ,
,
∴不等式![]() 等价于
等价于![]() ,
,
依题意知不等式![]() 的解集为
的解集为![]() ,
,
∴![]() 且1和2为方程
且1和2为方程![]() 的两根,
的两根,
∴ ,
,
解得 ,
,
∴实数![]() 、
、![]() 的值分别为
的值分别为![]() 、
、![]() ,
,
⑵不等式![]() 可化为
可化为![]() ,
,
(ⅰ)当![]() 时,不等式
时,不等式![]() 等价于
等价于![]() ,解得
,解得![]() ,故原不等式的解集为
,故原不等式的解集为![]() , 7分
, 7分
(ⅱ)当![]() 时,不等式
时,不等式![]() 等价于
等价于![]() ,
,
①当![]() 时
时![]() ,不等式
,不等式![]() 的解集为
的解集为![]() ,即原不等式的解集为
,即原不等式的解集为![]() ,
,
②当![]() 时,不等式
时,不等式![]() 的解集为
的解集为![]() ,即原不等式的解集为
,即原不等式的解集为![]() ,
,
③当![]() 时
时![]() ,不等式
,不等式![]() 的解集为
的解集为![]() ,即原不等式的解集为
,即原不等式的解集为![]() ,
,
(ⅲ)当![]() 时,不等式
时,不等式![]() 等价于
等价于![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴不等式![]() 的解集为
的解集为![]() ,即原不等式的解集为
,即原不等式的解集为![]() ,
,
综上所述,当![]() 时不等式
时不等式![]() 的的解集为
的的解集为![]() ,
,
当![]() 时不等式
时不等式![]() 的的解集为
的的解集为![]() ,
,
当![]() 时不等式
时不等式![]() 的的解集为
的的解集为![]() ,
,
当![]() 时不等式
时不等式![]() 的的解集为
的的解集为![]() ,
,
当![]() 时不等式
时不等式![]() 的的解集为
的的解集为![]() 。
。


科目:高中数学 来源: 题型:
【题目】(本小题满分13分)
如图,⊙O在平面![]() 内,AB是⊙O的直径,
内,AB是⊙O的直径,![]() 平面
平面![]() ,C为圆周上不同于A、B的任意一点,M,N,Q分别是PA,PC,PB的中点.
,C为圆周上不同于A、B的任意一点,M,N,Q分别是PA,PC,PB的中点.

(1)求证:![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)求证:![]() 平面
平面![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的首项a1=2,且an=2an﹣1﹣1(n∈N* , N≥2)
(1)求证:数列{an﹣1}为等比数列;并求数列{an}的通项公式;
(2)求数列{nan﹣n}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3﹣3ax2﹣9a2x+a3 . 若a> ![]() ,且当x∈[1,4a]时,|f′(x)|≤12a恒成立,则a的取值范围为( )
,且当x∈[1,4a]时,|f′(x)|≤12a恒成立,则a的取值范围为( )
A.( ![]() ,
, ![]() ]
]
B.( ![]() ,1]
,1]
C.[﹣ ![]() ,1]
,1]
D.[0, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三数学竞赛初赛考试后,对考生的成绩进行统计(考生成绩均不低于90分,满分150分),将成绩按如下方式分成六组,第一组[90,100)、第二组[100,110)…第六组[140,150].图(1)为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人. (Ⅰ)请补充完整频率分布直方图,并估计这组数据的平均数M;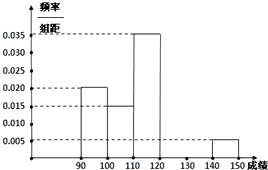
(Ⅱ)若不低于120分的同学进入决赛,不低于140分的同学为种子选手,完成下面2×2
列联表(即填写空格处的数据),并判断是否有99%的把握认为“进入决赛的同学
成为种子选手与专家培训有关”.
| [140,150] | 合计 | |
参加培训 | 5 | 8 | |
未参加培训 | |||
合计 | 4 |
附: ![]()
P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的参数方程为 ![]() (θ为参数).以原点O为极点,x轴的非负半轴为极轴建立极坐标方程.
(θ为参数).以原点O为极点,x轴的非负半轴为极轴建立极坐标方程.
(1)求曲线C的极坐标方程;
(2)若直线l:θ=α(α∈[0,π),ρ∈R)与曲线C相交于A,B两点,设线段AB的中点为M,求|OM|的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com