
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() .
.
(1)求证:数列![]() 为等比数列;
为等比数列;
(2)若![]() ,求
,求![]() 的前
的前![]() 项和
项和![]() .
.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)利用 ,化简得
,化简得![]() ,故
,故![]() 是等比数列;(2)由于
是等比数列;(2)由于![]() ,相等于一个等差数列乘以一个等比数列,所以考虑用错位相减求和法求前
,相等于一个等差数列乘以一个等比数列,所以考虑用错位相减求和法求前![]() 项和为
项和为![]() .
.
试题解析:
(1)当![]() 时,
时,![]() ,解得
,解得![]() ;...............1分
;...............1分
当![]() 时,
时,![]() ,两式相减得
,两式相减得![]() ,................3分
,................3分
化简得![]() ,所以数列
,所以数列![]() 是首项为1,公比为-1的等比数列..........5分
是首项为1,公比为-1的等比数列..........5分
(2)由(1)可得![]() ,所以
,所以![]() ,下提供三种求和方法供参考:.......6分
,下提供三种求和方法供参考:.......6分
【错位相减法】![]() ,
,
![]() ....................8分
....................8分
两式相减得![]() ................9分
................9分
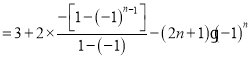 ....................10分
....................10分
![]() ,....................11分
,....................11分
所以数列![]() 的前
的前![]() 项和
项和![]() .........................12分
.........................12分
【并项求和法】/p>
当![]() 为偶数时,
为偶数时,![]() ;........................9分
;........................9分
当![]() 为奇数时,
为奇数时,![]() 为偶数,
为偶数,![]() ;............11分
;............11分
综上,数列![]() 的前
的前![]() 项和
项和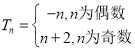 .........................12分
.........................12分
【裂项相消法】
因为![]() ..............9分
..............9分
所以![]()
![]() ,
,
所以数列![]() 的前
的前![]() 项和
项和![]() ..................12分
..................12分


科目:高中数学 来源: 题型:
【题目】某校从参加高一年级期末考试的学生中抽出60名学生,将其物理成绩(均为整数)分成六段![]() ,
, ![]() …
…![]() 后画出如下频率分布直方图.观察图形的信息,回答下列问题:
后画出如下频率分布直方图.观察图形的信息,回答下列问题:
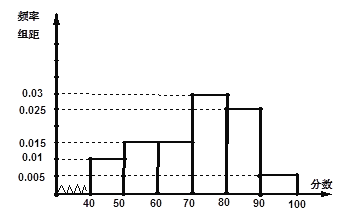
(Ⅰ)估计这次考试的众数m与中位数n(结果保留一位小数);
(Ⅱ) 估计这次考试的及格率(60分及以上为及格)和平均分.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂第一季度某产品月生产量依次为10万件,12万件,13万件,为了预测以后每个月的产量,以这3个月的产量为依据,用一个函数模拟该产品的月产量![]() (单位:万件)与月份
(单位:万件)与月份![]() 的关系. 模拟函数
的关系. 模拟函数![]() ;模拟函数
;模拟函数![]() .
.
(1)已知4月份的产量为万件,问选用哪个函数作为模拟函数好?
(2)受工厂设备的影响,全年的每月产量都不超过15万件,请选用合适的模拟函数预测6月份的产量.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
如图,在五棱锥![]() 中,
中,![]() ,且
,且![]() .
.
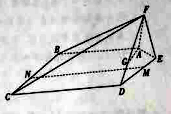
(1)已知点![]() 在线段
在线段![]() 上,确定
上,确定![]() 的位置,使得
的位置,使得![]() ;
;
(2)点![]() 分别在线段
分别在线段![]() 上,若沿直线
上,若沿直线![]() 将四边形
将四边形![]() 向上翻折,
向上翻折,![]() 与
与![]() 恰好重合,求直线
恰好重合,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的年销售量![]() 与该年广告费用支出
与该年广告费用支出![]() 有关,现收集了4组观测数据列于下表:
有关,现收集了4组观测数据列于下表:
| 1 | 4 | 5 | 6 |
| 30 | 40 | 60 | 50 |
现确定以广告费用支出![]() 为解释变量,销售量
为解释变量,销售量![]() 为预报变量对这两个变量进行统计分析.
为预报变量对这两个变量进行统计分析.
(1)已知这两个变量满足线性相关关系,试建立![]() 与
与![]() 之间的回归方程;
之间的回归方程;
(2)假如2017年广告费用支出为10万元,请根据你得到的模型,预测该年的销售量![]() .
.
(线性回归方程系数公式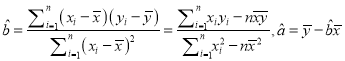 ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
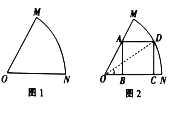
【题目】某车间为了制作某个零件,需从一块扇形的钢板余料(如图1)中按照图2的方式裁剪一块矩形钢板![]() ,其中顶点
,其中顶点![]() 、
、![]() 在半径
在半径![]() 上,顶点
上,顶点![]() 在半径
在半径![]() 上,顶点
上,顶点![]() 在
在![]() 上,
上, ![]() ,
, ![]() .设
.设![]() ,矩形
,矩形![]() 的面积为
的面积为![]() .
.
(1)用含![]() 的式子表示
的式子表示![]() ,
, ![]() 的长;
的长;
(2)试将![]() 表示为
表示为![]() 的函数;
的函数;
(3)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
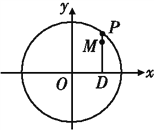
【题目】如图,设P是圆![]() 上的动点,点D是P在x轴上的投影,M为线段PD上一点,且
上的动点,点D是P在x轴上的投影,M为线段PD上一点,且![]() ,
,
(1)当P在圆上运动时,求点M的轨迹C的方程;
(2)求过点(3,0)且斜率为![]() 的直线被轨迹C所截线段的长度.
的直线被轨迹C所截线段的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 满足:①圆心在第一象限,截
满足:①圆心在第一象限,截![]() 轴所得弦长为2;②被
轴所得弦长为2;②被![]() 轴分成两段圆弧,其弧长的比为
轴分成两段圆弧,其弧长的比为![]() ;③圆心到直线
;③圆心到直线![]() 的距离为
的距离为![]() .
.
(Ⅰ)求圆![]() 的方程;
的方程;
(Ⅱ)若点![]() 是直线
是直线![]() 上的动点,过点
上的动点,过点![]() 分别做圆
分别做圆![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,
, ![]() ,求证:直线
,求证:直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系![]() 中,椭圆
中,椭圆![]() :
:![]() (
(![]() )的离心率是
)的离心率是![]() ,抛物线
,抛物线![]() :
:![]() 的焦点
的焦点![]() 是
是![]() 的一个顶点.
的一个顶点.
(1)求椭圆![]() 的方程;
的方程;
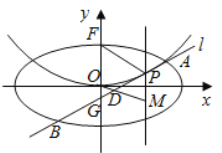
(2)设![]() 是
是![]() 上的动点,且位于第一象限,
上的动点,且位于第一象限,![]() 在点
在点![]() 处的切线
处的切线![]() 与
与![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,线段
,线段![]() 的中点为
的中点为![]() ,直线
,直线![]() 与过
与过![]() 且垂直于
且垂直于![]() 轴的直线交于点
轴的直线交于点![]() .
.
(i)求证:点![]() 在定直线上;
在定直线上;
(ii)直线![]() 与
与![]() 轴交于点
轴交于点![]() ,记△
,记△![]() 的面积为
的面积为![]() ,△
,△![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值及取得最大值时点
的最大值及取得最大值时点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com