
【题目】已知函数![]() (
(![]() 为实常数).
为实常数).

(1)当![]() 时,作出
时,作出![]() 的图象,并写出它的单调递增区间;
的图象,并写出它的单调递增区间;
(2)设![]() 在区间
在区间![]() 的最小值为
的最小值为![]() ,求
,求![]() 的表达式;
的表达式;
(3)已知函数![]() 在
在![]() 的情况下:其在区间
的情况下:其在区间![]() 单调递减,在区间
单调递减,在区间![]() 单调递增.设
单调递增.设![]() ,若函数
,若函数![]() 在区间
在区间![]() 上是增函数,求实数
上是增函数,求实数![]() 的取值范围.
的取值范围.
【答案】(1)图象见解析;单调递增区间![]() ;(2)
;(2)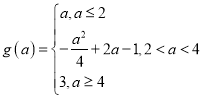 ;(3)
;(3)![]()
【解析】
(1)将二次函数![]() 图象在
图象在![]() 轴下方的部分沿
轴下方的部分沿![]() 轴翻折到
轴翻折到![]() 轴上方即可得到所求函数的图象,结合图象可写出单调递增区间;
轴上方即可得到所求函数的图象,结合图象可写出单调递增区间;
(2)根据二次函数对称轴为![]() ,分别讨论
,分别讨论![]() ,
,![]() 和
和![]() 三种情况,结合二次函数性质可得到三种情况下的最小值,进而得到
三种情况,结合二次函数性质可得到三种情况下的最小值,进而得到![]() ;
;
(3)当![]() 时,可知
时,可知![]() 为增函数,满足题意;当
为增函数,满足题意;当![]() 时,由已知所给函数的单调性可得
时,由已知所给函数的单调性可得![]() 单调性,进而构造不等式求得
单调性,进而构造不等式求得![]() 的范围;综合两种情况可得最终结果.
的范围;综合两种情况可得最终结果.
(1)当![]() 时,
时,![]() ,则
,则![]() 图象如下图所示:
图象如下图所示:

由图象可知:![]() 的单调递增区间为
的单调递增区间为![]()
(2)当![]() ,即
,即![]() 时,
时,![]()
当![]() ,即
,即![]() 时,
时,![]()
当![]() ,即
,即![]() 时,
时,![]()
综上所述: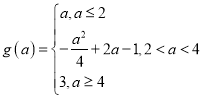
(3)由题意得:![]()
当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上单调递增,符合题意;
上单调递增,符合题意;
当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增
单调递增
![]() ,解得:
,解得:![]()
综上所述:实数![]() 的取值范围为
的取值范围为![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() :
:![]() ,直线
,直线![]() :
:![]() .
.
(1)求曲线![]() 和直线
和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 的直角坐标为
的直角坐标为![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量指数AQI是一种反映和评价空气质量的方法,AQI指数与空气质量对应如表所示:
AQI | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | 300以上 |
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
如图是某城市2018年12月全月的AQI指数变化统计图:

根据统计图判断,下列结论正确的是( )
A. 整体上看,这个月的空气质量越来越差
B. 整体上看,前半月的空气质量好于后半个月的空气质量
C. 从AQI数据看,前半月的方差大于后半月的方差
D. 从AQI数据看,前半月的平均值小于后半月的平均值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图1是由矩形![]() 和菱形
和菱形![]() 组成的一个平面图形,其中
组成的一个平面图形,其中![]() ,
, ![]() ,将其沿
,将其沿![]() 折起使得
折起使得![]() 与
与![]() 重合,连结
重合,连结![]() ,如图2.
,如图2.
(1)证明图2中的![]() 四点共面,且平面
四点共面,且平面![]() 平面
平面![]() ;
;
(2)求图2中的四边形![]() 的面积.
的面积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于实数a,b,定义运算“*”:a*b=![]() ,设f (x)=(x-4)*
,设f (x)=(x-4)*![]() ,若关于x的方程|f (x)-m|=1(m∈R)恰有四个互不相等的实数根,则实数m的取值范围是________.
,若关于x的方程|f (x)-m|=1(m∈R)恰有四个互不相等的实数根,则实数m的取值范围是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】二手车经销商小王对其所经营的![]() 型号二手汽车的使用年数
型号二手汽车的使用年数![]() 与销售价格
与销售价格![]() (单位:万元/辆)进行整理,得到如下数据:
(单位:万元/辆)进行整理,得到如下数据:
使用年数 |
|
|
|
|
|
|
售价 |
|
|
|
|
|
|
|
|
|
|
|
|
|
下面是![]() 关于
关于![]() 的折线图:
的折线图:

(1)由折线图可以看出,可以用线性回归模型拟合![]() 与
与![]() 的关系,请用相关系数加以说明;
的关系,请用相关系数加以说明;
(2)求![]() 关于
关于![]() 的回归方程并预测某辆
的回归方程并预测某辆![]() 型号二手车当使用年数为
型号二手车当使用年数为![]() 年时售价约为多少?(
年时售价约为多少?(![]() 、
、![]() 小数点后保留两位有效数字)
小数点后保留两位有效数字)
(3)基于成本的考虑,该型号二手车的售价不得低于![]() 元,请根据(2)求出的回归方程预测在收购该型号二手车时车辆的使用年数不得超过多少年?
元,请根据(2)求出的回归方程预测在收购该型号二手车时车辆的使用年数不得超过多少年?
参考数据:
![]() ,
,![]() ,
,![]() ,
,
 ,
, ,
,
 ,
,![]() ,
,![]() .
.
参考公式:回归直线方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
 ,
,![]() .
.
 ,
,![]() 、
、![]() 为样本平均值.
为样本平均值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com