
【题目】已知![]() 为等差数列,
为等差数列,![]() 为等比数列,
为等比数列,![]() .
.
(Ⅰ)求![]() 和
和![]() 的通项公式;
的通项公式;
(Ⅱ)记![]() 的前
的前![]() 项和为
项和为![]() ,求证:
,求证:![]() ;
;
(Ⅲ)对任意的正整数![]() ,设
,设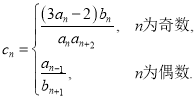 求数列
求数列![]() 的前
的前![]() 项和.
项和.
【答案】(Ⅰ)![]() ,
,![]() ;(Ⅱ)证明见解析;(Ⅲ)
;(Ⅱ)证明见解析;(Ⅲ)![]() .
.
【解析】
(Ⅰ)由题意分别求得数列的公差、公比,然后利用等差、等比数列的通项公式得到结果;
(Ⅱ)利用(Ⅰ)的结论首先求得数列![]() 前n项和,然后利用作差法证明即可;
前n项和,然后利用作差法证明即可;
(Ⅲ)分类讨论n为奇数和偶数时数列的通项公式,然后分别利用指数型裂项求和和错位相减求和计算![]() 和
和![]() 的值,据此进一步计算数列
的值,据此进一步计算数列![]() 的前2n项和即可.
的前2n项和即可.
(Ⅰ)设等差数列![]() 的公差为
的公差为![]() ,等比数列
,等比数列![]() 的公比为q.
的公比为q.
由![]() ,
,![]() ,可得d=1.
,可得d=1.
从而![]() 的通项公式为
的通项公式为![]() .
.
由![]() ,
,
又q≠0,可得![]() ,解得q=2,
,解得q=2,
从而![]() 的通项公式为
的通项公式为![]() .
.
(Ⅱ)证明:由(Ⅰ)可得![]() ,
,
故![]() ,
,![]() ,
,
从而![]() ,
,
所以![]() .
.
(Ⅲ)当n为奇数时,![]() ,
,
当n为偶数时,![]() ,
,
对任意的正整数n,有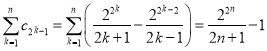 ,
,
和![]() ①
①
由①得![]() ②
②
由①②得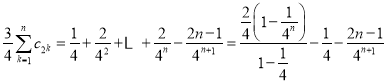 ,
,
由于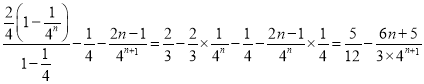 ,
,
从而得:![]() .
.
因此,![]() .
.
所以,数列![]() 的前2n项和为
的前2n项和为![]() .
.


科目:高中数学 来源: 题型:
【题目】某城市对一项惠民市政工程满意程度(分值:![]() 分)进行网上调查,有2000位市民参加了投票,经统计,得到如下频率分布直方图(部分图):
分)进行网上调查,有2000位市民参加了投票,经统计,得到如下频率分布直方图(部分图):

现用分层抽样的方法从所有参与网上投票的市民中随机抽取![]() 位市民召开座谈会,其中满意程度在
位市民召开座谈会,其中满意程度在![]() 的有5人.
的有5人.
(1)求![]() 的值,并填写下表(2000位参与投票分数和人数分布统计);
的值,并填写下表(2000位参与投票分数和人数分布统计);
满意程度(分数) |
|
|
|
|
|
人数 |
(2)求市民投票满意程度的平均分(各分数段取中点值);
(3)若满意程度在![]() 的5人中恰有2位为女性,座谈会将从这5位市民中任选两位发言,求男性甲或女性乙被选中的概率.
的5人中恰有2位为女性,座谈会将从这5位市民中任选两位发言,求男性甲或女性乙被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】CES是世界上最大的消费电子技术展,也是全球最大的消费技术产业盛会.2020CES消费电子展于2020年1月7日—10日在美国拉斯维加斯举办.在这次CES消费电子展上,我国某企业发布了全球首款彩色水墨屏阅读手机,惊艳了全场.若该公司从7名员工中选出3名员工负责接待工作(这3名员工的工作视为相同的工作),再选出2名员工分别在上午、下午讲解该款手机性能,若其中甲和乙至多有1人负责接待工作,则不同的安排方案共有__________种.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年春节期间,某超市准备举办一次有奖促销活动,若顾客一次消费达到400元则可参加一次抽奖活动,超市设计了两种抽奖方案.
方案一:一个不透明的盒子中装有30个质地均匀且大小相同的小球,其中10个红球,20个白球,搅拌均匀后,顾客从中随机抽取一个球,若抽到红球则顾客获得60元的返金券,若抽到白球则获得20元的返金券,且顾客有放回地抽取3次.
方案二:一个不透明的盒子中装有30个质地均匀且大小相同的小球,其中10个红球,20个白球,搅拌均匀后,顾客从中随机抽取一个球,若抽到红球则顾客获得80元的返金券,若抽到白球则未中奖,且顾客有放回地抽取3次.
(1)现有两位顾客均获得抽奖机会,且都按方案一抽奖,试求这两位顾客均获得180元返金券的概率;
(2)若某顾客获得抽奖机会.
①试分别计算他选择两种抽奖方案最终获得返金券的数学期望;
②为了吸引顾客消费,让顾客获得更多金额的返金券,该超市应选择哪一种抽奖方案进行促销活动?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的首项a1=1,前n项和为Sn.设λ与k是常数,若对一切正整数n,均有
的首项a1=1,前n项和为Sn.设λ与k是常数,若对一切正整数n,均有![]() 成立,则称此数列为“λ~k”数列.
成立,则称此数列为“λ~k”数列.
(1)若等差数列![]() 是“λ~1”数列,求λ的值;
是“λ~1”数列,求λ的值;
(2)若数列![]() 是“
是“![]() ”数列,且an>0,求数列
”数列,且an>0,求数列![]() 的通项公式;
的通项公式;
(3)对于给定的λ,是否存在三个不同的数列![]() 为“λ~3”数列,且an≥0?若存在,求λ的取值范围;若不存在,说明理由,
为“λ~3”数列,且an≥0?若存在,求λ的取值范围;若不存在,说明理由,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图①,在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() .
.![]() ,交
,交![]() 于点
于点![]() .将
.将![]() 沿线段
沿线段![]() 折起,使得点
折起,使得点![]() 在平面
在平面![]() 内的投影恰好是点
内的投影恰好是点![]() ,如图.
,如图.
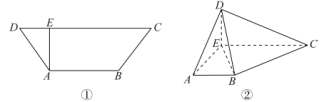
(1)若点![]() 为棱
为棱![]() 上任意一点,证明:平面
上任意一点,证明:平面![]() 平面
平面![]() .
.
(2)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得三棱锥
,使得三棱锥![]() 的体积为
的体积为![]() ?若存在,确定
?若存在,确定![]() 点的位置;若不存在,请说明理由.
点的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 、
、![]() 是抛物线
是抛物线![]() 上的两个不同的点,
上的两个不同的点,![]() 是坐标原点,若直线
是坐标原点,若直线![]() 与
与![]() 的斜率之积为
的斜率之积为![]() ,则下列结论正确的是( )
,则下列结论正确的是( )
A.![]()
B.以![]() 为直径的圆面积的最小值为
为直径的圆面积的最小值为![]()
C.直线![]() 过抛物线
过抛物线![]() 的焦点
的焦点
D.点![]() 到直线
到直线![]() 的距离不大于
的距离不大于![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com