
【题目】在△ABC中,a,b,c分别为内角A,B,C的对边,且(2b﹣c)cosA=acosC.
(1)求A;
(2)若△ABC的面积为![]() ,求a的最小值.
,求a的最小值.
【答案】(1)A![]() .(2)a的最小值为2.
.(2)a的最小值为2.
【解析】
(1)由正弦定理将(2b﹣c)cosA=acosC,转化为(2sinB﹣sinC)cosA=sinAcosC,再利用两角和的正弦公式求解.
(2)根据A![]() 和△ABC的面积为
和△ABC的面积为![]() bcsinA
bcsinA![]() bc,求得bc=4,由余弦定理得a2=b2+c2﹣2bccosA=b2+c2﹣bc,再利用基本不等式求解.
bc,求得bc=4,由余弦定理得a2=b2+c2﹣2bccosA=b2+c2﹣bc,再利用基本不等式求解.
(1)∵(2b﹣c)cosA=acosC,
∴由正弦定理可得:(2sinB﹣sinC)cosA=sinAcosC,
∴2sinBcosA=sinCcosA+sinAcosC=sin(A+C)=sinB,
∵sinB≠0,
∴cosA![]() ,
,
∵A∈(0,π),
∴A![]() .
.
(2)∵A![]() ,△ABC的面积为
,△ABC的面积为![]() bcsinA
bcsinA![]() bc,
bc,
∴bc=4,
∴a2=b2+c2﹣2bccosA=b2+c2﹣bc≥2bc﹣bc=bc=4,
解得a≥2,当且仅当b=c=2时等号成立,
∴a的最小值为2.


科目:高中数学 来源: 题型:
【题目】已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=2,F为CD的中点.
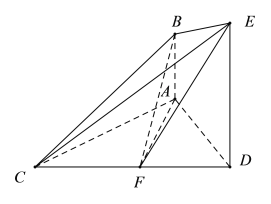
(1)求证:面BCE⊥面DCE;
(2)求二面角C﹣BE﹣F的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的导函数为
的导函数为![]() ,且对任意的实数
,且对任意的实数![]() 都有
都有![]() (
(![]() 是自然对数的底数),且
是自然对数的底数),且![]() ,若关于
,若关于![]() 的不等式
的不等式![]() 的解集中恰有唯一一个整数,则实数
的解集中恰有唯一一个整数,则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:x2=2py(p>0)的焦点为(0,1)
(1)求抛物线C的方程;
(2)设直线l2:y=kx+m与抛物线C有唯一公共点P,且与直线l1:y=﹣1相交于点Q,试问,在坐标平面内是否存在点N,使得以PQ为直径的圆恒过点N?若存在,求出点N的坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点P是△PMN的顶点,M(﹣2,0),N(2,0),直线PM,PN的斜率之积为﹣![]() .
.
(1)求点P的轨迹E的方程;
(2)设四边形ABCD的顶点都在曲线E上,且AB∥CD,直线AB,CD分别过点(﹣1,0),(1,0),求四边形ABCD的面积为![]() 时,直线AB的方程.
时,直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,其中
,其中![]() N
N![]() ,
,![]() ≥2,且
≥2,且![]() R.
R.
(1)当![]() ,
,![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,令
时,令![]() ,若函数
,若函数![]() 有两个极值点
有两个极值点![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)当![]() 时,试求函数
时,试求函数![]() 的零点个数,并证明你的结论.
的零点个数,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
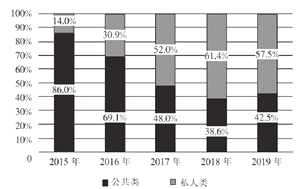
【题目】如图统计了截止2019年年底中国电动车充电桩细分产品占比及保有量情况,关于这5次统计,下列说法正确的是( )
中国电动车充电桩细分产品占比情况:
中国电动车充电桩细分产品保有量情况:(单位:万台)
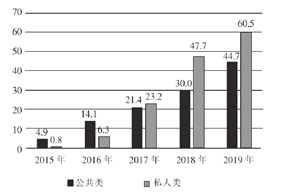
A.私人类电动汽车充电桩保有量增长率最高的年份是2018年
B.公共类电动汽车充电桩保有量的中位数是25.7万台
C.公共类电动汽车充电桩保有量的平均数为23.12万台
D.从2017年开始,我国私人类电动汽车充电桩占比均超过![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com