
【题目】已知函数![]() ,满足
,满足![]() .设
.设![]() 为
为![]() 上任一点,过
上任一点,过![]() 作
作![]() 的切线,其斜率
的切线,其斜率![]() 满足
满足![]()
(1)求函数![]() 的解析式;
的解析式;
(2)若数列![]() 满足
满足![]() .设
.设![]() 为正常数.
为正常数.
①求![]() ;
;
②若不等式![]() 对任意的
对任意的![]() 恒成立,则实数
恒成立,则实数![]() 是否存在最大值?若存在,请求出这个值;若不存在,请说明理由.
是否存在最大值?若存在,请求出这个值;若不存在,请说明理由.
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() (
(![]() )的左右焦点分别为
)的左右焦点分别为![]() ,
, ![]() ,若椭圆上一点
,若椭圆上一点![]() 满足
满足![]() ,且椭圆
,且椭圆![]() 过点
过点![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于两点
交于两点![]()
![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作
作![]() 轴的垂线,交椭圆
轴的垂线,交椭圆![]() 于
于![]() ,求证:
,求证: ![]() ,
, ![]() ,
, ![]() 三点共线.
三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A,B两种移动支付方式的使用情况,从全校所有的1000名学生中随机抽取了100人,发现样本中A,B两种支付方式都不使用的有5人,样本中仅使用A和仅使用B的学生的支付金额分布情况如下:
支付方式 | 不大于2000元 | 大于2000元 |
仅使用A | 27人 | 3人 |
仅使用B | 24人 | 1人 |
(Ⅰ)估计该校学生中上个月A,B两种支付方式都使用的人数;
(Ⅱ)从样本仅使用B的学生中随机抽取1人,求该学生上个月支付金额大于2000元的概率;
(Ⅲ)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用B的学生中随机抽查1人,发现他本月的支付金额大于2000元.结合(Ⅱ)的结果,能否认为样本仅使用B的学生中本月支付金额大于2000元的人数有变化?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
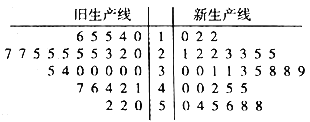
【题目】近几年,我国鲜切花产业得到了快速发展,相关部门制定了鲜切花产品行业等级标准,统一使用综合指标值![]() 进行衡量,如下表所示.某花卉生产基地准备购进一套新型的生产线,现进行设备试用,分别从新旧两条生产线加工的产品中选取30个样品进行等级评定,整理成如图所示的茎叶图.
进行衡量,如下表所示.某花卉生产基地准备购进一套新型的生产线,现进行设备试用,分别从新旧两条生产线加工的产品中选取30个样品进行等级评定,整理成如图所示的茎叶图.
综合指标 |
|
|
|
质量等级 | 三级 | 二级 | 一级 |
(Ⅰ)根据茎叶图比较两条生产线加工的产品的综合指标值的平均值及分散程度(直接给出结论即可);
(Ⅱ)若从等级为三级的样品中随机选取3个进行生产流程调查,其中来自新型生产线的样品个数为![]() ,求
,求![]() 的分布列;
的分布列;
(Ⅲ)根据该花卉生产基地的生产记录,原有生产线加工的产品的单件平均利润为4元,产品的销售率(某等级产品的销量与产量的比值)及产品售价如下表:
三级花 | 二级花 | 一级花 | |
销售率 |
|
|
|
单件售价 | 12元 | 16元 | 20元 |
预计该新型生产线加工的鲜切花单件产品的成本为10元,日产量3000件.因为鲜切花产品的保鲜特点,未售出的产品统一按原售价的50%全部处理完.如果仅从单件产品利润的角度考虑,该生产基地是否需要引进该新型生产线?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() ,…,
,…,![]() 为取自某总体的样本,其算术平均值称为样本均值,一般用
为取自某总体的样本,其算术平均值称为样本均值,一般用![]() 表示,即
表示,即![]() ,在分组样本场合,样本均值的近似公式为
,在分组样本场合,样本均值的近似公式为![]() ,其中k为组数,
,其中k为组数,![]() 为第i组的组中值,
为第i组的组中值,![]() 为第i组的频数.某单位收集到20名青年的某天娱乐支出费用数据:
为第i组的频数.某单位收集到20名青年的某天娱乐支出费用数据:
79 84 84 88 92 93 94 97 98 99
100 101 101 102 102 108 110 113 118 125
若将分为五组,第一组为![]() ,根据分组样本计算样本均值为( )
,根据分组样本计算样本均值为( )
A.99.4B.143.16C.100D.11.96
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() ,
,![]() ,数列
,数列![]() 满足
满足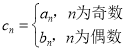 ,n
,n![]() .
.
(1)若![]() ,
,![]() ,求数列
,求数列![]() 的前2n项和
的前2n项和![]() ;
;
(2)若数列![]() 为等差数列,且对任意n
为等差数列,且对任意n![]() ,
,![]() 恒成立.
恒成立.
①当数列![]() 为等差数列时,求证:数列
为等差数列时,求证:数列![]() ,
,![]() 的公差相等;
的公差相等;
②数列![]() 能否为等比数列?若能,请写出所有满足条件的数列
能否为等比数列?若能,请写出所有满足条件的数列![]() ;若不能,请说明理由.
;若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】BMI指数是用体重公斤数除以身高米数的平方得出的数值,是国际上常用的衡量人体胖瘦程度以及是否健康的一个标准.对于高中男体育特长生而言,当BMI数值大于或等于20.5时,我们说体重较重,当BMI数值小于20.5时,我们说体重较轻,身高大于或等于170cm时,我们说身高较高,身高小于170cm时,我们说身高较矮.某中小学生成长与发展机构从某市的320名高中男体育特长生中随机选取8名,其身高和体重的数据如表所示:
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
身高(cm) | 166 | 167 | 160 | 173 | 178 | 169 | 158 | 173 |
体重(kg) | 57 | 58 | 53 | 61 | 66 | 57 | 50 | 66 |
(1)根据最小二乘法的思想与公式求得线性回归方程![]() .利用已经求得的线性回归方程,请完善下列残差表,并求解释变量(身高)对于预报变量(体重)变化的贡献值
.利用已经求得的线性回归方程,请完善下列残差表,并求解释变量(身高)对于预报变量(体重)变化的贡献值![]() (保留两位有效数字);
(保留两位有效数字);
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
身高(cm) | 166 | 167 | 160 | 173 | 178 | 169 | 158 | 173 |
体重(kg) | 57 | 58 | 53 | 61 | 66 | 57 | 50 | 66 |
残差 | 0.1 | 0.3 | 0.9 | ﹣1.5 | ﹣0.5 |
(2)通过残差分析,对于残差的最大(绝对值)的那组数据,需要确认在样本点的采集中是否有人为的错误.已知通过重新采集发现,该组数据的体重应该为58(kg).请重新根据最小二乘法的思想与公式,求出男体育特长生的身高与体重的线性回归方程.
参考公式: 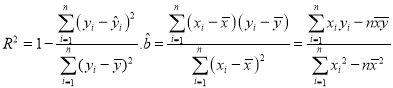 ,
,![]() .
.![]() .
.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com