
【题目】已知数列{an}中,a1=1,a3=9,且an=an﹣1+λn﹣1(n≥2).
(1)求λ的值及数列{an}的通项公式;
(2)设 ![]() ,且数列{bn}的前n项和为Sn , 求S2n .
,且数列{bn}的前n项和为Sn , 求S2n .
【答案】
(1)解:∵a1=1,a3=9,且an=an﹣1+λn﹣1(n≥2),∴a2=2λ,a3=5λ﹣1=9,解得λ=2.
∴an﹣an﹣1=2n﹣1(n≥2).
∴an=(2n﹣1)+(2n﹣3)+…+3+1= ![]() =n2.
=n2.
(2)解: ![]() =(﹣1)n(n2+n),
=(﹣1)n(n2+n),
b2n﹣1+b2n=﹣[(2n﹣1)2+(2n﹣1)]+[(2n)2+2n]=4n.
S2n=4× ![]() =2n2+2n
=2n2+2n
【解析】(I)a1=1,a3=9,且an=an﹣1+λn﹣1(n≥2),可得a2=2λ,a3=5λ﹣1=9,解得λ.可得an﹣an﹣1=2n﹣1(n≥2).利用“累加求和”方法即可得出.(II) ![]() =(﹣1)n(n2+n),可得b2n﹣1+b2n=﹣[(2n﹣1)2+(2n﹣1)]+[(2n)2+2n]=4n.即可得出S2n .
=(﹣1)n(n2+n),可得b2n﹣1+b2n=﹣[(2n﹣1)2+(2n﹣1)]+[(2n)2+2n]=4n.即可得出S2n .


科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A.![]() 是
是 ![]() 或
或 ![]() 的充分不必要条件
的充分不必要条件
B.若命题 ![]() ,则
,则 ![]()
C.线性相关系数 ![]() 的绝对值越接近1,表示两变量的相关性越强
的绝对值越接近1,表示两变量的相关性越强
D.用频率分布直方图估计平均数,可以用每个小矩形的高乘以底边中点横坐标之和
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把函数 ![]() 的图象上每个点的横坐标扩大到原来的4倍,再向左平移
的图象上每个点的横坐标扩大到原来的4倍,再向左平移 ![]() ,得到函数g(x)的图象,则函数g(x)的一个单调递减区间为( )
,得到函数g(x)的图象,则函数g(x)的一个单调递减区间为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直三棱柱ABC﹣A1B1C1的底面为正三角形,E,F分别是A1C1 , B1C1上的点,且满足A1E=EC1 , B1F=3FC1 . 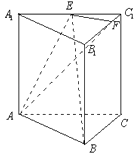
(1)求证:平面AEF⊥平面BB1C1C;
(2)设直三棱柱ABC﹣A1B1C1的棱长均相等,求二面角C1﹣AE﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,已知点P( ![]() ,1),直线l的参数方程为
,1),直线l的参数方程为 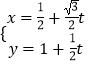 (t为参数)若以O为极点,以Ox为极轴,选择相同的单位长度建立极坐标系,则曲线C的极坐标方程为ρ=
(t为参数)若以O为极点,以Ox为极轴,选择相同的单位长度建立极坐标系,则曲线C的极坐标方程为ρ= ![]() cos(θ-
cos(θ- ![]() )
)
(Ⅰ)求直线l的普通方程和曲线C的直角坐标方程;
(Ⅱ)设直线l与曲线C相交于A,B两点,求点P到A,B两点的距离之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把函数 ![]() 的图象上每个点的横坐标扩大到原来的4倍,再向左平移
的图象上每个点的横坐标扩大到原来的4倍,再向左平移 ![]() ,得到函数g(x)的图象,则函数g(x)的一个单调递减区间为( )
,得到函数g(x)的图象,则函数g(x)的一个单调递减区间为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种水果的单个质量在500g以上视为特等品.随机抽取1000个该水果,结果有50个特等品.将这50个水果的质量数据分组,得到下边的频率分布表.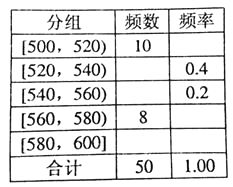
(1)估计该水果的质量不少于560g的概率;
(2)若在某批水果的检测中,发现有15个特等品,据此估计该批水果中没有达到特等品的个数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com