
设函数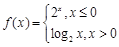 ,若对任意给定的
,若对任意给定的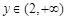 ,都存在唯一的
,都存在唯一的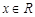 ,满足
,满足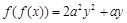 ,则正实数
,则正实数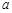 的最小值是( )
的最小值是( )
A.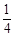 | B.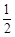 | C.2 | D.4 |
A
解析试卷分析:首先写出f(f(x))表达式,当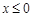 时,
时,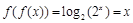 ;当
;当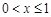 时,
时,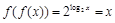 ;当
;当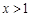 时,
时,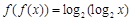 ,考虑到题目说的要求x的唯一性,即当取某个y值时,f(f(x))的值只能落在三段区间的一段,而不能落在其中的两段或者三段内。因此我们要先求出f(f(x))在每段区间的值域。当
,考虑到题目说的要求x的唯一性,即当取某个y值时,f(f(x))的值只能落在三段区间的一段,而不能落在其中的两段或者三段内。因此我们要先求出f(f(x))在每段区间的值域。当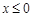 时,
时,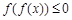 ;当
;当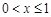 时,
时,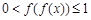 ;当
;当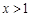 时,
时, 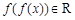 .从中可发现,上面两段区间的值包含在最后一段区间内,换一句话就是说假如f(f(x))取在小于等于1的范围内的任何一个值,则必有两个x与之对应。因此,考虑到x的唯一性,则只有使得f(f(x))>1,因此题目转化为当y>2时,恒有
.从中可发现,上面两段区间的值包含在最后一段区间内,换一句话就是说假如f(f(x))取在小于等于1的范围内的任何一个值,则必有两个x与之对应。因此,考虑到x的唯一性,则只有使得f(f(x))>1,因此题目转化为当y>2时,恒有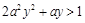 。因此令
。因此令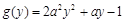 ,题目转化为y>2时,恒有g(y)>0,又g(y)=(2ay-1)(ay+1),为了要使其大于0,则
,题目转化为y>2时,恒有g(y)>0,又g(y)=(2ay-1)(ay+1),为了要使其大于0,则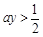 或
或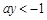 ,考虑到题目要求a的正实数,则ay<-1不考虑。因此
,考虑到题目要求a的正实数,则ay<-1不考虑。因此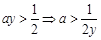 ,在y大于2的情况下恒成立。因此
,在y大于2的情况下恒成立。因此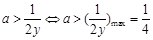 ,所以a的最小正实数为
,所以a的最小正实数为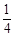 (因为y本身取不到2,因此a可以取
(因为y本身取不到2,因此a可以取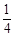 ).
).
考点:1.指数与对数的运算;2.不等式恒成立问题;3.函数的值域.


科目:高中数学 来源: 题型:单选题
已知a>0,且a≠1,loga3<1,则实数a的取值范围是( )
| A.(0,1) | B.(0,1)∪(3,+∞) |
| C.(3,+∞) | D.(1,2)∪(3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
设f(x)与g(x)是定义在同一区间[a,b]上的两个函数,若函数y=f(x)-g(x)在x∈[a,b]上有两个不同的零点,则称f(x)和g(x)在[a,b]上是“关联函数”,区间[a,b]称为“关联区间”.若f(x)=x2-3x+4与g(x)=2x+m在[0,3]上是“关联函数”,则m的取值范围是 ( ).
A. | B.[-1,0] | C.(-∞,-2] | D. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com