分析:(Ⅰ)通过求导即可得到切线的斜率,进而得到切线的方程,即可得到xn+1与xn的关系,利用等比数列的通项公式即可求出.
(Ⅱ)利用三角形的面积公式、梯形的面积公式及(Ⅰ)的结论即可得出;
(Ⅲ)利用(Ⅰ)的结论即可求出nkn,再利用“错位相减法”即可求出Sn,进而证明结论.
解答:解:(Ⅰ)∵
y′=-,∴f
′(1)=-1,
∴曲线C:
y=在点P(1,1)处的切线为y-1=-(x-1),
令y=0,则x=2,∴Q
1(2,0),∴
P1(2,),∴x
1=2.
则过点
Pn(xn,)的切线斜率为
-,其方程为
y-=-(x-xn),
令y=0,得到x=2x
n,∴Q
n+1(2x
n,0),即x
n+1=2x
n,∴
=2.
∴数列{x
n}是以2为首项,2为公比的等比数列,
∴
xn=2×2n-1=2n.
(Ⅱ)∵
S△OPnPn+1=
S△OPnQn+S梯形PnPn+1Qn+1Qn-
S△OPn+1Qn+1=
xnyn+(xn+1-xn)-
xn+1yn+1=
(+)(xn+1-xn)=
(+)(2n+1-2n)=
.
(Ⅲ)证明:由(1)可知:k
n=
=
=
=
,∴nk
n=
.
∴S
n=
+++…+
+,
4S
n=
1+++…+
,
两式相减得3S
n═1+
+
+…+
-
=
-
,
∴S
n=
--<.
故
Sn<成立.
点评:熟练掌握导数的几何意义、等比数列的通项公式及其前n项和公式、“错位相减法”是解题的关键.

 如图,已知曲线C:y=
如图,已知曲线C:y=

 名校课堂系列答案
名校课堂系列答案 如图,已知曲线C:y=
如图,已知曲线C:y=
 (2006•南京二模)如图,已知曲线C:y=
(2006•南京二模)如图,已知曲线C:y=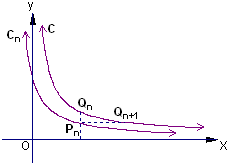 如图,已知曲线C:y=
如图,已知曲线C:y= 如图,已知曲线C:y=x2(0≤x≤1),O(0,0),Q(1,0),R(1,1).取线段OQ的中点A1,过A1作x轴的垂线交曲线C于P1,过P1作y轴的垂线交RQ于B1,记a1为矩形A1P1B1Q的面积.分别取线段OA1,P1B1的中点A2,A3,过A2,A3分别作x轴的垂线交曲线C于P2,P3,过P2,P3分别作y 轴的垂线交A1P1,RB1于B2,B3,记a2为两个矩形A2P2B2A1与矩形A3P3B3B1的面积之和.以此类推,记an为2n-1个矩形面积之和,从而得数列{an},设这个数列的前n项和为Sn.
如图,已知曲线C:y=x2(0≤x≤1),O(0,0),Q(1,0),R(1,1).取线段OQ的中点A1,过A1作x轴的垂线交曲线C于P1,过P1作y轴的垂线交RQ于B1,记a1为矩形A1P1B1Q的面积.分别取线段OA1,P1B1的中点A2,A3,过A2,A3分别作x轴的垂线交曲线C于P2,P3,过P2,P3分别作y 轴的垂线交A1P1,RB1于B2,B3,记a2为两个矩形A2P2B2A1与矩形A3P3B3B1的面积之和.以此类推,记an为2n-1个矩形面积之和,从而得数列{an},设这个数列的前n项和为Sn.