
【题目】某校为了解高三年级不同性别的学生对体育课改上自习课的态度(肯定还是否定),进行了如下的调查研究.全年级共有![]() 名学生,男女生人数之比为
名学生,男女生人数之比为![]() ,现按分层抽样方法抽取若干名学生,每人被抽到的概率均为
,现按分层抽样方法抽取若干名学生,每人被抽到的概率均为![]() .
.
(1)求抽取的男学生人数和女学生人数;
(2)通过对被抽取的学生的问卷调查,得到如下![]() 列联表:
列联表:
否定 | 肯定 | 总计 | |
男生 | 10 | ||
女生 | 30 | ||
总计 |
①完成列联表;
②能否有![]() 的把握认为态度与性别有关?
的把握认为态度与性别有关?
(3)若一班有![]() 名男生被抽到,其中
名男生被抽到,其中![]() 人持否定态度,
人持否定态度,![]() 人持肯定态度;二班有
人持肯定态度;二班有![]() 名女生被抽到,其中
名女生被抽到,其中![]() 人持否定态度,
人持否定态度,![]() 人持肯定态度.
人持肯定态度.
现从这![]() 人中随机抽取一男一女进一步询问所持态度的原因,求其中恰有一人持肯定态度一人持否定态度的概率.
人中随机抽取一男一女进一步询问所持态度的原因,求其中恰有一人持肯定态度一人持否定态度的概率.
解答时可参考下面临界值表:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
【答案】(1)55,50
(2) ①
否定 | 肯定 | 总计 | |
男生 | 45 | 10 | 55 |
女生 | 30 | 20 | 50 |
总计 | 75 | 30 | 105 |
有![]() 的把握认为态度与性别有关
的把握认为态度与性别有关
(3)0.5
【解析】
试题解:(1)共抽取![]() 人, 1分
人, 1分
男生![]() 人, 女生
人, 女生![]() 人, 3分
人, 3分
(2)①
否定 | 肯定 | 总计 | |
男生 | 45 | 10 | 55 |
女生 | 30 | 20 | 50 |
总计 | 75 | 30 | 105 |
② 假设![]() : 学生对体育课改上自习课的态度与性别无关
: 学生对体育课改上自习课的态度与性别无关
![]()
因为![]() ,
,![]()
所以 有![]() 的把握认为态度与性别有关. 8分
的把握认为态度与性别有关. 8分
(3)记一班被抽到的男生为![]() ,
,![]() 持否定态度,
持否定态度,![]() 持肯定态度;
持肯定态度;
二班被抽到的女生为![]() ,
,![]() 持否定态度,
持否定态度,![]() 持肯定态度.
持肯定态度.
则所有抽取可能共有20种:![]() ,
,![]() ,
,![]() ,
,![]() ;
;![]() ,
,![]() ,
,![]() ,
,![]() ;
;![]() ,
,![]() ,
,![]() ,
,![]() ;
;![]() ,
,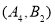 ,
,![]() ,
,![]() ;
;![]() ,
,![]() ,
,![]() ,
,![]() . 10分
. 10分
其中恰有一人持否定态度一人持肯定态度的有10种:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() . 11分
. 11分
记“从这![]() 人中随机抽取一男一女,其中恰有一人持肯定态度一人持否定态度”事件为
人中随机抽取一男一女,其中恰有一人持肯定态度一人持否定态度”事件为![]() ,则
,则![]() . 12分
. 12分
答:(1)抽取男生55人,女生50人;(2)有有![]() 的把握认为态度与性别有关;
的把握认为态度与性别有关;
(3)恰有一人持肯定态度一人持否定态度的概率为![]() . 13分
. 13分


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ;直线
;直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() ,
,![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)若点![]() 的极坐标为
的极坐标为![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】奇函数f(x)在R上存在导数![]() ,当x<0时,
,当x<0时,![]()
![]() f(x),则使得(x2﹣1)f(x)<0成立的x的取值范围为( )
f(x),则使得(x2﹣1)f(x)<0成立的x的取值范围为( )
A.(﹣1,0)∪(0,1)B.(﹣∞,﹣1)∪(0,1)
C.(﹣1,0)∪(1,+∞)D.(﹣∞,﹣1)∪(1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知幂函数f(x)=(3m2﹣2m)x![]() 在(0,+∞)上单调递增,g(x)=x2﹣4x+t.
在(0,+∞)上单调递增,g(x)=x2﹣4x+t.
(1)求实数m的值;
(2)当x∈[1,9]时,记f(x),g(x)的值域分别为集合A,B,设命题p:x∈A,命题q:x∈B,若命题q是命题p的必要不充分条件,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图甲,在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中点.将
的中点.将![]() 沿
沿![]() 折起,使二面角
折起,使二面角![]() 为
为![]() ,连接
,连接![]() ,
,![]() 得到四棱锥
得到四棱锥![]() (如图乙),
(如图乙),![]() 为
为![]() 的中点,
的中点,![]() 是棱
是棱![]() 上一点.
上一点.
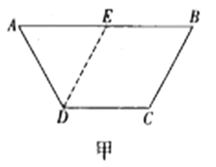
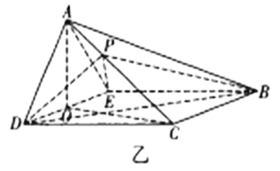
(1)求证:当![]() 为
为![]() 的中点时,平面
的中点时,平面![]() 平面
平面![]() ;
;
(2)是否存在一点![]() ,使平面
,使平面![]() 与平面
与平面![]() 所成的锐二面角为
所成的锐二面角为![]() ,若存在,求
,若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程是
的参数方程是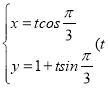 为参数),曲线
为参数),曲线![]() 的参数方程是
的参数方程是 为参数),以
为参数),以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)求直线![]() 和曲线
和曲线![]() 的极坐标方程;
的极坐标方程;
(2)已知射线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,射线
两点,射线![]() 与直线
与直线![]() 交于
交于![]() 点,若
点,若![]() 的面积为1,求
的面积为1,求![]() 的值和弦长
的值和弦长![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市旅游管理部门为提升该市26个旅游景点的服务质量,对该市26个旅游景点的交通、安全、环保、卫生、管理五项指标进行评分.每项评分最低分0分,最高分100分.每个景点总分为这五项得分之和,根据考核评分结果,绘制交通得分与安全得分散点图、交通得分与景点总分散点图如图
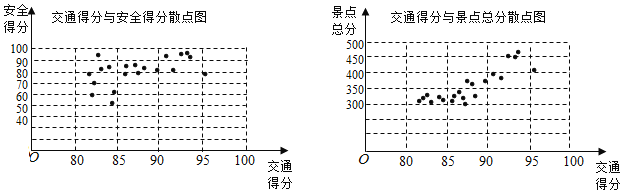
请根据图中所提供的信息,完成下列问题:
(1)若从交通得分排名前5名的景点中任取1个,求其安全得分大于90分的概率;
(2)若从景点总分排名前6名的景点中任取3个,记安全得分不大于90分的景点个数为ξ,求随机变量ξ的分布列和数学期望;
(3)记该市26个景点的交通平均得分为![]() ,安全平均得分为
,安全平均得分为![]() ,写出
,写出![]() 和
和![]() 的大小关系?(只写出结果)
的大小关系?(只写出结果)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com