
【题目】设b和c分别是先后抛掷一枚骰子得到的点数,用随机变量ξ表示方程x2+bx+c=0实根的个数(重根按一个计).
(1)求方程x2+bx+c=0有实根的概率;
(2)求ξ的分布列和数学期望;
(3)求在先后两次出现的点数中有5的条件下,方程x2+bx+c=0有实根的概率.
【答案】
(1)解:由题意知,本题是一个等可能事件的概率,
试验发生包含的基本事件总数为6×6=36,
满足条件的事件是使方程有实根,则△=b2﹣4c≥0,即 ![]() .
.
下面针对于c的取值进行讨论
当c=1时,b=2,3,4,5,6;
当c=2时,b=3,4,5,6;
当c=3时,b=4,5,6;
当c=4时,b=4,5,6;
当c=5时,b=5,6;
当c=6时,b=5,6,
目标事件个数为5+4+3+3+2+2=19,
因此方程x2+bx+c=0有实根的概率为 ![]() .
.
(2)解:由题意知用随机变量ξ表示方程x2+bx+c=0实根的个数得到ξ=0,1,2
根据第一问做出的结果得到
则 ![]() ,
, ![]() ,
, ![]() ,
,
∴ξ的分布列为
ξ | 0 | 1 | 2 |
P |
|
|
|
∴ξ的数学期望 ![]() .
.
(3)解:在先后两次出现的点数中有5的条件下,方程x2+bx+c=0有实根,
这是一个条件概率,
记“先后两次出现的点数中有5”为事件M,
“方程ax2+bx+c=0有实根”为事件N,
则 ![]() ,
, ![]() ,
,
∴ ![]() .
.
【解析】(1)由题意知,本题是一个等可能事件的概率,试验发生包含的基本事件总数为6×6,满足条件的事件是使方程有实根,则△=b2﹣4c≥0,对于c的取值进行列举,得到事件数,根据概率公式得到结果.(2)由题意知用随机变量ξ表示方程x2+bx+c=0实根的个数得到ξ的可能取值0,1,2根据第一问做出的结果写出变量对应的概率,写出分布列和期望.(3)在先后两次出现的点数中有5的条件下,方程x2+bx+c=0有实根,这是一个条件概率,做出先后两次出现的点数中有5的概率和先后两次出现的点数中有5的条件下且方程x2+bx+c=0有实根的概率,根据条件概率的公式得到结果.
【考点精析】本题主要考查了离散型随机变量及其分布列的相关知识点,需要掌握在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴,建立极坐标系.已知曲线C1: ![]() (t为参数),C2:
(t为参数),C2: ![]() (θ为参数).
(θ为参数).
(1)化C1 , C2的方程为普通方程,并说明它们分别表示什么曲线;
(2)若C1上的点P对应的参数为t= ![]() ,Q为C2上的动点,求PQ中点M到直线C3:ρ(cosθ﹣2sinθ)=7距离的最小值.
,Q为C2上的动点,求PQ中点M到直线C3:ρ(cosθ﹣2sinθ)=7距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,AB= ![]() =AC=2,E,F分别为A1C1 , BC的中点.
=AC=2,E,F分别为A1C1 , BC的中点. 
(1)求证:平面ABE⊥平面B1BCC1;
(2)求证:C1F∥平面ABE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,从2009年参加奥运知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如图所示.观察图形,估计这次奥运知识竞赛的及格率(大于或等于60分为及格)为 . 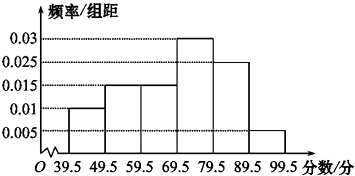
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校开设A、B、C、D、E五门选修课,要求每位同学彼此独立地从中选修3门课程.某甲同学必选A课程,不选B课程,另从其余课程中随机任选两门课程.乙、丙两名同学从五门课程中随机任选三门课程.
(1)求甲同学选中C课程且乙、丙同学未选C课程的概率;
(2)用X表示甲、乙、丙选中C课程的人数之和,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足an+1= ![]() an2﹣
an2﹣ ![]() nan+1(n∈N*),且a1=3.
nan+1(n∈N*),且a1=3.
(1)计算a2 , a3 , a4的值,由此猜想数列{an}的通项公式,并给出证明;
(2)求证:当n≥2时,ann≥4nn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com