
【题目】已知抛物线![]() 的焦点坐标为
的焦点坐标为![]() .
.
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)过点![]() 作互相垂直的直线
作互相垂直的直线![]() ,与抛物线
,与抛物线![]() 分别相交于
分别相交于![]() 两点和
两点和![]() 两点,求四边形
两点,求四边形![]() 面积的最小值.
面积的最小值.
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:
【题目】下列各式:
(1)已知loga ![]() <1,则a>
<1,则a> ![]() ;
;
(2)函数y=2x的图象与函数y=2﹣x的图象关于y轴对称;
(3)函数f(x)=lg(mx2+mx+1)的定义域是R,则m的取值范围是0≤m<4;
(4)函数y=ln(﹣x2+x)的递增区间为(﹣∞, ![]() ]
]
正确的有 . (把你认为正确的序号全部写上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年某市街头开始兴起“mobike”、“ofo”等共享单车,这样的共享单车为很多市民解决了最后一公里的出行难题.然而,这种模式也遇到了一些让人尴尬的问题,比如乱停乱放,或将共享单车占为“私有”等.为此,某机构就是否支持发展共享单车随机调查了50人,他们年龄的分布及支持发展共享单车的人数统计如下表:
年龄 |
|
|
|
|
|
|
受访人数 | 5 | 6 | 15 | 9 | 10 | 5 |
支持发展共享单车人数 | 4 | 5 | 12 | 9 | 7 | 3 |
(Ⅰ)由以上统计数据填写下面的![]() 列联表,并判断能否在犯错误的概率不超过0.1的前提下,认为年龄与是否支持发展共享单车有关系:
列联表,并判断能否在犯错误的概率不超过0.1的前提下,认为年龄与是否支持发展共享单车有关系:
年龄低于35岁 | 年龄不低于35岁 | 合计 | |
支持 | |||
不支持 | |||
合计 |
(Ⅱ)若对年龄在![]() 的被调查人中随机选取两人,对年龄在
的被调查人中随机选取两人,对年龄在![]() 的被调查人中随机选取一人进行调查,求选中的3人中支持发展共享单车的人数为2人的概率.
的被调查人中随机选取一人进行调查,求选中的3人中支持发展共享单车的人数为2人的概率.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式: 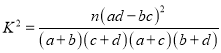 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂每日生产一种大型产品1件,每件产品的投入成本为2000元.产品质量为一等品的概率为![]() ,二等品的概率为
,二等品的概率为![]() ,每件一等品的出厂价为10000元,每件二等品的出厂价为8000元.若产品质量不能达到一等品或二等品,除成本不能收回外,没生产一件产品还会带来1000元的损失.
,每件一等品的出厂价为10000元,每件二等品的出厂价为8000元.若产品质量不能达到一等品或二等品,除成本不能收回外,没生产一件产品还会带来1000元的损失.
(1)求在连续生产3天中,恰有一天生产的两件产品都为一等品的的概率;
(2)已知该厂某日生产的2件产品中有一件为一等品,求另一件也为一等品的概率;
(3)求该厂每日生产该种产品所获得的利润![]() (元)的分布列及数学期望.
(元)的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某大学联盟的自主招生考试中,报考文史专业的考生参加了人文基础学科考试科目“语文”和“数学”的考试.某考场考生的两科考试成绩数据统计如下图所示,本次考试中成绩在![]() 内的记为
内的记为![]() ,其中“语文”科目成绩在
,其中“语文”科目成绩在![]() 内的考生有10人.
内的考生有10人.
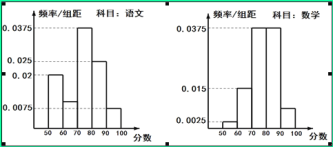
(1)求该考场考生数学科目成绩为![]() 的人数;
的人数;
(2)已知参加本考场测试的考生中,恰有2人的两科成绩均为![]() .在至少一科成绩为
.在至少一科成绩为![]() 的考生中,随机抽取2人进行访谈,求这2人的两科成绩均为
的考生中,随机抽取2人进行访谈,求这2人的两科成绩均为![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com