
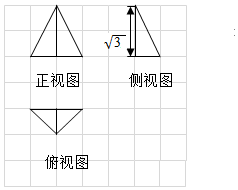
 网格纸的各小格都是边长为1的正方形,图中粗实线画出的是一个几何体的三视图,其中正视图是正三角形,则该几何体的外接球表面积为( )
网格纸的各小格都是边长为1的正方形,图中粗实线画出的是一个几何体的三视图,其中正视图是正三角形,则该几何体的外接球表面积为( )| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{4π}{3}$ | D. | $\frac{16π}{3}$ |
分析 该几何体是有一个侧面PAC垂直于底面,高为 $\sqrt{3}$,底面是一个等腰直角三角形的三棱锥,这个几何体的外接球的球心O在高线PD上,且是等边三角形PAC的中心,由此能求出这个几何体的外接球的半径R,从而能求出这个几何体的外接球的表面积.
解答  解:由已知中正视图是一个正三角形,侧视图和俯视图均为三角形,
解:由已知中正视图是一个正三角形,侧视图和俯视图均为三角形,
可得该几何体是有一个侧面PAC垂直于底面,高为 $\sqrt{3}$,
底面是一个等腰直角三角形的三棱锥,如图.
则这个几何体的外接球的球心O在高线PD上,
且是等边三角形PAC的中心,
这个几何体的外接球的半径R=$\frac{2}{3}$PD=$\frac{2\sqrt{3}}{3}$.
则这个几何体的外接球的表面积为S=4πR2=4π×($\frac{2\sqrt{3}}{3}$)2=$\frac{16π}{3}$.
故选:D.
点评 本题考查几何体的外接球的表面积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:选择题
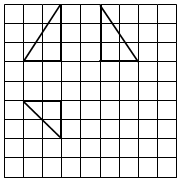 如图,网络纸上正方形的边长为l,粗线画出的是某几何体的三视图,则该几何体的外接球表面积为( )
如图,网络纸上正方形的边长为l,粗线画出的是某几何体的三视图,则该几何体的外接球表面积为( )| A. | 12π | B. | 34π | C. | $\frac{17π}{4}$ | D. | 17π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到如图部分频率分布直方图.观察图形的信息,回答下列问题.
某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到如图部分频率分布直方图.观察图形的信息,回答下列问题.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{16}{3}$ | B. | 32 | C. | $\frac{32}{3}$ | D. | $\frac{64}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<c<b | B. | a<b<c | C. | b<a<c | D. | c<b<a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com