
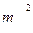 的厂房(不管墙高),工程的造价是:
的厂房(不管墙高),工程的造价是:科目:高中数学 来源:不详 题型:解答题
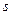 km,汽车从甲地匀速行驶到乙地,速度不得超过
km,汽车从甲地匀速行驶到乙地,速度不得超过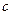 km/h,已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度
km/h,已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度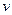 km/h的平方成正比,比例系数为
km/h的平方成正比,比例系数为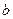 ,固定部分为
,固定部分为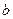 元.
元.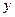 (元)表示为
(元)表示为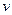 速度(千米/时)的函数,并指出这个函数的定义域;
速度(千米/时)的函数,并指出这个函数的定义域;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
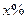 ,则销售量将减少
,则销售量将减少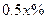 ,且该品牌汽车每台的价格上涨幅度不超过
,且该品牌汽车每台的价格上涨幅度不超过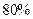 ,问当该品牌汽车每台的价格上涨百分之几,可使销售的总金额最大?
,问当该品牌汽车每台的价格上涨百分之几,可使销售的总金额最大?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
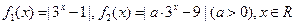 ,
, 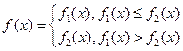 .
.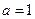 时,求
时,求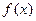 在
在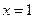 处的切线方程;
处的切线方程;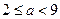 时,设
时,设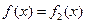 所对应的自变量取值区间的长度为
所对应的自变量取值区间的长度为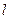 (闭区间
(闭区间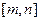 的长度定义为
的长度定义为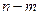 ),试求
),试求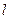 的最大值;
的最大值;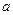 ,使得当
,使得当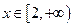 时,
时,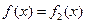 ?若存在,求出
?若存在,求出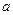 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
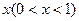 ,那么月平均销售量减少的百分率为
,那么月平均销售量减少的百分率为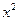 ,记改进工艺后,该公司销售纪念品的月平均利润是y(元)。
,记改进工艺后,该公司销售纪念品的月平均利润是y(元)。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
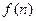 表示前
表示前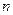 年的纯利润总和,
年的纯利润总和, 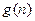 表示前
表示前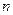 年的总支出.
年的总支出. 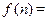 前
前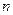 年的总收入-前
年的总收入-前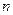 年的总支出-投资额].
年的总支出-投资额].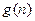 的关系式
的关系式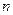 年的纯利润总和
年的纯利润总和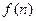 关于
关于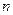 的函数关系式;并求该厂从第几年开始盈利?
的函数关系式;并求该厂从第几年开始盈利?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com