
【题目】已知在平面直角坐标系xOy中,过点P(1,0)的直线l的参数方程是  (t是参数),以原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C点的极坐标方程为ρ=﹣4sin(θ﹣
(t是参数),以原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C点的极坐标方程为ρ=﹣4sin(θ﹣ ![]() ).
).
(1)判断直线l与曲线C的位置关系;
(2)若直线l与曲线C交于两点A、B,求|PA||PB|的值.
【答案】
(1)解:直线l的参数方程是 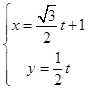 (t是参数),消去参数t可得普通方程:x﹣
(t是参数),消去参数t可得普通方程:x﹣ ![]() y﹣1=0.
y﹣1=0.
曲线C点的极坐标方程为ρ=﹣4sin(θ﹣ ![]() ),即ρ2=﹣4ρsin(θ﹣
),即ρ2=﹣4ρsin(θ﹣ ![]() ),可得直角坐标方程:x2+y2+4×
),可得直角坐标方程:x2+y2+4× 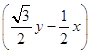 =0,
=0,
配方为(x﹣1)2+ ![]() =4,可得圆心C(1,﹣
=4,可得圆心C(1,﹣ ![]() ),半径r=2.
),半径r=2.
圆心到直线l的距离d= 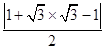 =
= ![]() <2=r.
<2=r.
∴直线l与曲线C的位置关系是相交
(2)解:把直线l的参数方程 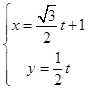 (t是参数),代入圆C的方程可得:t2+
(t是参数),代入圆C的方程可得:t2+ ![]() t﹣1=0.
t﹣1=0.
∴t1t2=﹣1.
∴|PA||PB|=|t1t2|=1
【解析】(1)直线l的参数方程是 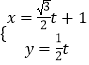 (t是参数),消去参数t可得普通方程.曲线C点的极坐标方程为ρ=﹣4sin(θ﹣
(t是参数),消去参数t可得普通方程.曲线C点的极坐标方程为ρ=﹣4sin(θ﹣ ![]() ),即ρ2=﹣4ρsin(θ﹣
),即ρ2=﹣4ρsin(θ﹣ ![]() ),利用互化公式可得直角坐标方程.求出圆心到直线l的距离d,与半径r比较可得直线l与曲线C的位置关系.(2)把直线l的参数方程
),利用互化公式可得直角坐标方程.求出圆心到直线l的距离d,与半径r比较可得直线l与曲线C的位置关系.(2)把直线l的参数方程 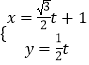 (t是参数),代入圆C的方程可得:t2+
(t是参数),代入圆C的方程可得:t2+ ![]() t﹣1=0.可得|PA||PB|=|t1t2|.
t﹣1=0.可得|PA||PB|=|t1t2|.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:高中数学 来源: 题型:
【题目】在极坐标系中,圆C的极坐标方程为:ρ2=4ρ(cosθ+sinθ)﹣3.若以极点O为原点,极轴所在直线为x轴建立平面直角坐标系.
(Ⅰ)求圆C的参数方程;
(Ⅱ)在直角坐标系中,点P(x,y)是圆C上动点,试求x+2y的最大值,并求出此时点P的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四面体ABCD中,二面角A﹣BC﹣D为60°,点P为直线BC上一动点,记直线PA与平面BCD所成的角为θ,则( ) 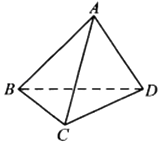
A.θ的最大值为60°
B.θ的最小值为60°
C.θ的最大值为30°
D.θ的最小值为30°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥中P﹣ABCD,PA⊥平面ABCD,AD∥BC,AD⊥CD,且AD=CD=2 ![]() ,BC=4
,BC=4 ![]() ,PA=2.
,PA=2. 
(1)求证:AB⊥PC;
(2)在线段PD上,是否存在一点M,使得二面角M﹣AC﹣D的大小为45°,如果存在,求BM与平面MAC所成角的正弦值,如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂为了解用电量y与气温x℃之间的关系,随机统计了5天的用电量与当天气温,得到如下统计表:
曰期 | 8月1曰 | 8月7日 | 8月14日 | 8月18日 | 8月25日 |
平均气温(℃) | 33 | 30 | 32 | 30 | 25 |
用电量(万度) | 38 | 35 | 41 | 36 | 30 |
![]() xiyi=5446,
xiyi=5446, ![]() xi2=4538,
xi2=4538, ![]() =
= 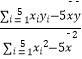 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
(1)请根据表中的数据,求出y关于x的线性回归方程.据气象預报9月3日的平均气温是 23℃,请预测9月3日的用电量;(结果保留整数)
(2)请从表中任选两天,记用电量(万度)超过35的天数为ξ,求ξ的概率分布列,并求其数学期望和方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2lnx﹣ax2+3,若存在实数m、n∈[1,5]满足n﹣m≥2时,f(m)=f(n)成立,则实数a的最大值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C1的参数方程是 ![]() (α为参数),以原点O为极点,x轴的正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为ρ=1.
(α为参数),以原点O为极点,x轴的正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为ρ=1.
(Ⅰ)分别写出C1的极坐标方程和C2的直角坐标方程;
(Ⅱ)若射线l的极坐标方程θ= ![]() (ρ≥0),且l分别交曲线C1、C2于A、B两点,求|AB|.
(ρ≥0),且l分别交曲线C1、C2于A、B两点,求|AB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知ω为正整数,函数f(x)=sinωxcosωx+ ![]() 在区间
在区间 ![]() 内单调递增,则函数f(x)( )
内单调递增,则函数f(x)( )
A.最小值为 ![]() ,其图象关于点
,其图象关于点 ![]() 对称
对称
B.最大值为 ![]() ,其图象关于直线
,其图象关于直线 ![]() 对称
对称
C.最小正周期为2π,其图象关于点 ![]() 对称
对称
D.最小正周期为π,其图象关于直线 ![]() 对称
对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将一张边长为12cm的正方形纸片按如图(1)所示阴影部分裁去四个全等的等腰三角形,将余下部分沿虚线折叠并拼成一个有底的正四棱锥模型,如图(2)所示放置.如果正四棱锥的主视图是等边三角形,如图(3)所示,则正四棱锥的体积是( ) 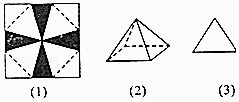
A.![]() cm3
cm3
B.![]() cm3
cm3
C.![]() cm3
cm3
D.![]() cm3
cm3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com