分析:(Ⅰ)求出函数f
3(x)的导函数,在定义域内根据导函数的符号判断原函数在不同区间内的单调性,由单调性分析极值;
(Ⅱ)由
fn()•fn()<0可知函数f
n(x)在区间
(,)上有零点,然后利用导函数的符号得到函数f
n(x)在区间
(,)上单调递增,从而得到答案.
解答:解:(Ⅰ)∵
f3(x)=x3-3x-1,∴
f3′(x)=3x2-3,
∵当x>1时,
f3′(x)>0;当0<x<1时,
f3′(x)<0.
∴当x=1时,f
3(x)取得极小值-3,无极大值;
(Ⅱ)函数f
n(x)在区间
(,)上有且只有一个零点.
证明:
∵
fn()=()3-n-1=-1<0,
fn()=()3-n-1=-1>0,
fn()•fn()<0,∴函数f
n(x)在区间
(,)上必定存在零点.
∵
fn′(x)=3x2-n,∴当
x∈(,)时,
fn′(x)>3()2-n=2n>0,
∴f
n(x)在区间
(,)上单调递增,
∴函数f
n(x)在区间
(,)上的零点最多一个.
综上知:函数f
n(x)在区间
(,)上存在唯一零点.
点评:本题主要考查函数在某点取得极值的条件,考查了零点存在性定理,单调函数在区间[a,b]上满足f(a)f(b)<0,则函数在区间(a,b)上有唯一零点,是中档题.



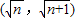 上零点的个数,并给予证明.
上零点的个数,并给予证明.