
分析 (Ⅰ)求出曲线y=f(x)在点P(2,f(2))处的导数值等于切线的斜率为-6,即可求实数a;
(Ⅱ)通过a=1,利用导函数为0,判断导数符号,即可求f(x)的极值;
(Ⅲ)当0<a<2时,利用导函数的单调性,通过f(x)在[1,4]上的最小值为-$\frac{16}{3}$,即可求出a,然后求f(x)在该区间上的最大值.
解答 (本小题满分14分)
解:(Ⅰ)因为f′(x)=-x2+x+2a,
曲线y=f(x)在点P(2,f(2))处的切线的斜率k=f′(2)=2a-2,-------------(3分)
依题意:2a-2=-6,a=-2.-------------(4分)
(Ⅱ)当a=1时,$f(x)=-\frac{1}{3}{x^3}+\frac{1}{2}{x^2}+2x$,f′(x)=-x2+x+2=-(x+1)(x-2)----(5分)
| x | (-∞,-1) | -1 | (-1,2) | 2 | (2,+∞) |
| f′(x) | - | 0 | + | 0 | - |
| f(x) | 单调减 | $-\frac{7}{6}$ | 单调增 | $\frac{10}{3}$ | 单调减 |
点评 本题考查导数的综合应用,切线方程以及极值的求法,函数的单调性与函数的最值的关系,考查转化思想以及计算能力.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:解答题
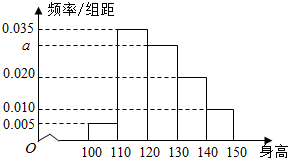 从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图),
从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图),查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{-1+2i}{3}$ | B. | $\frac{1+2i}{3}$ | C. | $\frac{1+2i}{5}$ | D. | $\frac{-1+2i}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 最小正周期为π | |
| B. | 函数y=sin2x向左平移$\frac{π}{12}$个单位可得到f(x) | |
| C. | f(x)在区间$(-\frac{π}{3},\frac{π}{6})$上递增 | |
| D. | 点$(\frac{π}{6},0)$是f(x)的一个对称中心 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
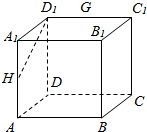 如图所示,在正方体ABCD-A1B1C1D1中,E、G、H分别是BC、C1D1、AA1、的中点.
如图所示,在正方体ABCD-A1B1C1D1中,E、G、H分别是BC、C1D1、AA1、的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com