
【题目】(1)求函数![]() 在
在![]() 的最大值;
的最大值;
(2)证明:函数![]() 在
在![]() 有两个极值点
有两个极值点![]() ,且
,且![]() .
.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)利用导数求出函数![]() 在
在![]() 上的单调性即可;
上的单调性即可;
(2)首先利用导数求出![]() 的单调性,即可得到
的单调性,即可得到![]() ,然后分别证明
,然后分别证明![]() ,
,![]() ,
,![]() ,然后即可证明
,然后即可证明![]() .
.
(1)![]() ,则
,则![]() 在
在![]() 上单调递增,
上单调递增,
又![]() ,
,
所以![]() 在
在![]() 有唯一的零点
有唯一的零点![]() .
.
当![]() 时,
时,![]() 单调递减;
单调递减;
![]() 时,
时,![]() 单调递增.
单调递增.
又![]() ,
,
所以![]() 在
在![]() 的最大值为
的最大值为![]() .
.
(2)![]() ,
,
则当![]() 时,
时,![]() 单调递增,
单调递增,
又![]() ,
,
所以![]() 在
在![]() 有唯一的零点
有唯一的零点![]() ,
,
此时,![]() 时,
时,![]() ;
;![]() 时,
时,![]() ,
,
所以![]() 是极小值点,不妨令
是极小值点,不妨令![]() .
.
当![]() 时,
时,![]() ,所以
,所以![]() ;
;
当![]() ,设
,设![]() .
.
由(1)知, ![]() 有唯一的零点
有唯一的零点![]() ,
,
则![]() 时,
时,![]() 单调递减,即
单调递减,即![]() 单调递减;
单调递减;
![]() 时,
时,![]() 单调递增,即
单调递增,即![]() 单调递增
单调递增
又![]() ,
,
所以![]() 在
在![]() 有唯一的零点
有唯一的零点![]() ,
,
此时![]() 时,
时,![]() ;
;![]() 时,
时,![]() ,
,
所以![]() 是极大值点,即
是极大值点,即![]() ,
,
所以![]() 在
在![]() 有两个极值点
有两个极值点![]() ,其中
,其中![]() ,
,![]() ,
,
且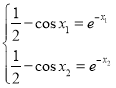 ,由于
,由于![]() ,所以
,所以![]() .
.
因为![]() ,
,![]() ,
,
所以![]() ,即
,即![]() .
.
又![]() ,所以
,所以![]() ,同理
,同理![]() ,
,
所以![]() .
. ![]() .
.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x22(a+2)x+a2,g(x)=x2+2(a2)xa2+8.设H1(x)=max{f(x),g(x)},H2(x)=min{f(x),g(x)}(max{p,q}表示p,q中的较大值,min{p,q}表示p,q中的较小值).记H1(x)的最小值为A,H2(x)的最大值为B,则AB=( )
A.a22a16B.a2+2a16
C.16D.16
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知线段![]() 是过抛物线
是过抛物线![]() 的焦点F的一条弦,过点A(A在第一象限内)作直线
的焦点F的一条弦,过点A(A在第一象限内)作直线![]() 垂直于抛物线的准线,垂足为C,直线
垂直于抛物线的准线,垂足为C,直线![]() 与抛物线相切于点A,交x轴于点T,给出下列命题:
与抛物线相切于点A,交x轴于点T,给出下列命题:
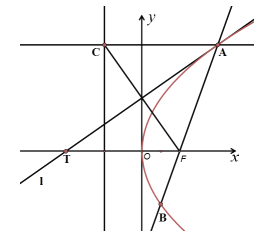
(1)![]() ;
;
(2)![]() ;
;
(3)![]() .
.
其中正确的命题个数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】法国的数学家费马(PierredeFermat)曾在一本数学书的空白处写下一个看起来很简单的猜想:当整数![]() 时,找不到满足
时,找不到满足![]() 的正整数解.该定理史称费马最后定理,也被称为费马大定理.费马只是留下这个叙述并且说他已经发现这个定理的证明妙法,只是书页的空白处不够无法写下.费马也因此为数学界留下了一个千古的难题,历经数代数学家们的努力,这个难题直到1993年才由我国的数学家毛桂成完美解决,最终证明了费马大定理的正确性.现任取
的正整数解.该定理史称费马最后定理,也被称为费马大定理.费马只是留下这个叙述并且说他已经发现这个定理的证明妙法,只是书页的空白处不够无法写下.费马也因此为数学界留下了一个千古的难题,历经数代数学家们的努力,这个难题直到1993年才由我国的数学家毛桂成完美解决,最终证明了费马大定理的正确性.现任取![]() ,则等式
,则等式![]() 成立的概率为( )
成立的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为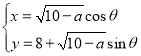 (
(![]() 为参数,常数
为参数,常数![]() ).以坐标原点为极点,
).以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,已知直线
轴的正半轴为极轴建立极坐标系,已知直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出![]() 及直线
及直线![]() 的直角坐标方程,并指出
的直角坐标方程,并指出![]() 是什么曲线;
是什么曲线;
(2)设![]() 是曲线
是曲线![]() 上的一个动点,求点
上的一个动点,求点![]() 到直线
到直线![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】武汉某商场为促进市民消费,准备每周随机的从十个热门品牌中抽取一个品牌送消费券,并且某个品牌被抽中后不再参与后面的抽奖,没有抽中的品牌则继续参加下周抽奖,假设每次抽取时各品牌被抽到的可能性相同,每次抽取也相互独立.
(1)求某品牌到第三次才被抽到的概率;
(2)为了使更多品牌参加活动,商场做出调整,从第一周抽取后开始每周会有一个新的品牌补充进抽取队伍,品牌A从第一周就开始参加抽奖,商场准备开展半年(按26周计算)的抽奖活动,记品牌A参与抽奖的次数为X,试求X的数学期望(精确到0.01).
参考数据:![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com