
【题目】在直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() ,若圆
,若圆![]()
![]() 的一条切线与椭圆
的一条切线与椭圆![]() 有两个交点
有两个交点![]() ,且
,且![]() .
.
(1)求圆![]() 的方程;
的方程;
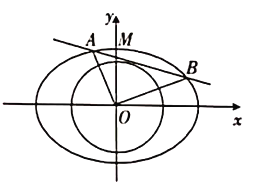
(2)已知椭圆![]() 的上顶点为
的上顶点为![]() ,点
,点![]() 在圆
在圆![]() 上,直线
上,直线![]() 与椭圆
与椭圆![]() 相交于另一点
相交于另一点![]() ,且
,且![]() ,求直线
,求直线![]() 的方程.
的方程.
 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:
【题目】一批用于手电筒的电池,每节电池的寿命服从正态分布![]() (寿命单位:小时).考虑到生产成本,电池使用寿命在
(寿命单位:小时).考虑到生产成本,电池使用寿命在![]() 内是合格产品.
内是合格产品.
(1)求一节电池是合格产品的概率(结果四舍五入,保留一位小数);
(2)根据(1)中的数据结果,若质检部门检查4节电池,记抽查电池合格的数量为![]() ,求随机变量
,求随机变量![]() 的分布列、数学期望及方差.
的分布列、数学期望及方差.
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三1班共有48人,在“六选三”时,该班共有三个课程组合:理化生、理化历、史地政其中,选择理化生的共有24人,选择理化历的共有16人,其余人选择了史地政,现采用分层抽样的方法从中抽出6人,调查他们每天完成作业的时间.
(1)应从这三个组合中分别抽取多少人?
(2)若抽出的6人中有4人每天完成六科(含语数英)作业所需时间在3小时以上,2人在3小时以内.现从这6人中随机抽取3人进行座谈.
用X表示抽取的3人中每天完成作业所需时间在3小时以上的人数,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】党的十八大指出,倡导富强、民主、文明、和谐,倡导自由、平等、公正、法治,倡导爱国、敬业、诚信、友善.现在从“民主”、“文明”、“自由”、“公正”、“爱国”、“敬业”这6个词语中任选2个,则“至少有一个词语是从国家层面对社会主义核心价值观基本理念的凝练”的概率是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,已知抛物线
中,已知抛物线![]()
![]() 上一点
上一点![]() 到焦点
到焦点![]() 的距离为6,点
的距离为6,点![]() 为其准线
为其准线![]() 上的任意一点,过点
上的任意一点,过点![]() 作抛物线
作抛物线![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)当点![]() 在
在![]() 轴上时,证明:
轴上时,证明:![]() 为等腰直角三角形.
为等腰直角三角形.
(3)证明:![]() 为直角三角形.
为直角三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() .
.
(1)若![]() ,求函数
,求函数![]() 的单调区间;
的单调区间;
(2)若![]() ,且函数
,且函数![]() 在区间
在区间![]() 内有两个极值点,求实数a的取值范围;
内有两个极值点,求实数a的取值范围;
(3)求证:对任意的正数a,都存在实数t,满足:对任意的![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com