
【题目】已知函数![]()
(1)若![]() 的图象在点
的图象在点![]() 处的切线方程为
处的切线方程为![]() ,求
,求![]() 在区间[-2,4]上的最大值;
在区间[-2,4]上的最大值;
(2)当![]() 时,若
时,若![]() 在区间(-1,1)上不单调,求
在区间(-1,1)上不单调,求![]() 的取值范围.
的取值范围.
【答案】.解:(Ⅰ)![]() …………………………………………1分
…………………………………………1分
![]() ………………………………2分
………………………………2分
∴a=0或2. ………………………………………………………………………4分
(Ⅱ)∵(1,f(1))是切点,∴1+f(1)-3=0, ∴f(1)=2…………………5分
![]()
∵切线方程x+y-3=0的斜率为-1,
![]() ……………………………7分
……………………………7分
![]()
![]() …………8分
…………8分![]() ……………………………………9分
……………………………………9分
∴y=f(x)在区间[-2,4]上的最大值为8. …………………………………………10分
(Ⅲ)因为函数f(x)在区间(-1,1)不单调,所以函数![]() 在(-1,1)上存在零点.
在(-1,1)上存在零点.
而![]() =0的两根为a-1,a+1,区间长为2,
=0的两根为a-1,a+1,区间长为2,
∴在区间(-1,1)上不可能有2个零点. ……………………………11分
![]() ………………………………12分
………………………………12分
![]()
![]() ……………………………………………14分
……………………………………………14分
【解析】
(1)先利用![]() 的图象在点
的图象在点![]() 处的切线方程为
处的切线方程为![]() 求出
求出![]() ,再求函数
,再求函数![]() 在区间
在区间![]() 上的最大值.(2)由题得
上的最大值.(2)由题得![]() 得
得![]() 或
或![]() ,再解不等式
,再解不等式![]() 或
或 ![]() 得解.
得解.
(1)由已知得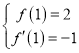 ,
, 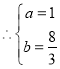 ,
,
![]() ,
, ![]() ,
,
令![]() , 得
, 得![]() 或2,
或2,
又![]()
![]()
![]() ,
, ![]() ,
,
![]() .
.
(2)![]() 得
得![]() 或
或![]() ,
,
若![]() 在
在![]() 上不单调,则
上不单调,则![]() 在
在![]() 上有解,
上有解,
![]() 或
或 ![]() ,
,
![]() 或
或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,某污水处理厂要在一个矩形污水处理池![]() 的池底水平铺设污水净化管道(
的池底水平铺设污水净化管道(![]() ,H是直角顶点)来处理污水,管道越短,铺设管道的成本越低.设计要求管道的接口H是
,H是直角顶点)来处理污水,管道越短,铺设管道的成本越低.设计要求管道的接口H是![]() 的中点,点E,F分别落在线段
的中点,点E,F分别落在线段![]() 上.已知
上.已知![]() ,记
,记![]() .
.

(1)试将污水管道的长度表示为![]() 的函数,并写出定义域;
的函数,并写出定义域;
(2)已知![]() ,求此时管道的长度l;
,求此时管道的长度l;
(3)当![]() 取何值时,铺设管道的成本最低?并求出此时管道的长度.
取何值时,铺设管道的成本最低?并求出此时管道的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:若数列![]() 和
和![]() 满足
满足![]() 则称数列
则称数列![]() 是数列
是数列![]() 的“伴随数列”.
的“伴随数列”.
已知数列![]() 是数列
是数列![]() 的伴随数列,试解答下列问题:
的伴随数列,试解答下列问题:
(1)若![]() ,
,![]() ,求数列
,求数列![]() 的通项公式
的通项公式![]() ;
;
(2)若![]() ,
,![]() 为常数,求证:数列
为常数,求证:数列![]() 是等差数列;
是等差数列;
(3)若![]() ,数列
,数列![]() 是等比数列,求
是等比数列,求![]() 的数值.
的数值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设三次函数f(x)=ax3+bx2+cx+1的导函数为f![]() (x)=3ax(x-2),若函数y=f(x)共有三个不同的零点,则a的取值范围是( )
(x)=3ax(x-2),若函数y=f(x)共有三个不同的零点,则a的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】世界那么大,我想去看看,每年高考结束后,处于休养状态的高中毕业生旅游动机强烈,旅游可支配收入日益增多,可见高中毕业生旅游是一个巨大的市场.为了解高中毕业生每年旅游消费支出(单位:百元)的情况,相关部门随机抽取了某市的1000名毕业生进行问卷调查,并把所得数据列成如下所示的频数分布表:
组别 |
|
|
|
|
|
频数 |
|
|
|
|
|
(1)求所得样本的中位数(精确到百元);
(2)根据样本数据,可近似地认为学生的旅游费用支出![]() 服从正态分布
服从正态分布![]() ,若该市共有高中毕业生35000人,试估计有多少位同学旅游费用支出在 8100元以上;
,若该市共有高中毕业生35000人,试估计有多少位同学旅游费用支出在 8100元以上;
(3)已知本数据中旅游费用支出在![]() 范围内的8名学生中有5名女生,3名男生, 现想选其中3名学生回访,记选出的男生人数为
范围内的8名学生中有5名女生,3名男生, 现想选其中3名学生回访,记选出的男生人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
附:若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面四边形ABCD中,已知A=![]() ,B=
,B=![]() ,AB=6.在AB边上取点E,使得BE=1,连接EC,ED.若∠CED=
,AB=6.在AB边上取点E,使得BE=1,连接EC,ED.若∠CED=![]() ,EC=
,EC=![]() .
.

(1)求sin∠BCE的值;
(2)求CD的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,若椭圆上一点
,若椭圆上一点![]() 满足
满足![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于两点
交于两点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作
作![]() 轴的垂线,交椭圆
轴的垂线,交椭圆![]() 于
于![]() ,求证:存在实数
,求证:存在实数![]() ,使得
,使得![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,
,![]() 分别是椭圆
分别是椭圆![]()
![]() 的长轴端点、短轴端点,
的长轴端点、短轴端点,![]() 为坐标原点,若
为坐标原点,若![]() ,
,![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)如果斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于不同的两点
于不同的两点![]() (都不同于点
(都不同于点![]() ),线段
),线段![]() 的中点为
的中点为![]() ,设线段
,设线段![]() 的垂线
的垂线![]() 的斜率为
的斜率为![]() ,试探求
,试探求![]() 与
与![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com