
【题目】.华为公司研发的5G技术是中国在高科技领域的重大创新,目前处于世界领先地位,今年即将投入使用,它必将为人们生活带来别样的精彩,成为每个中国人的骄傲.现假设在一段光纤中有![]() 条通信线路,需要输送
条通信线路,需要输送![]() 种数据包,每条线路单位时间内输送不同数据包的大小数值如表所示.若在单位时间内,每条线路只能输送一种数据包,且使完成
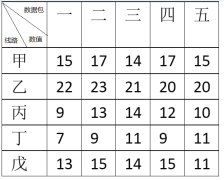
种数据包,每条线路单位时间内输送不同数据包的大小数值如表所示.若在单位时间内,每条线路只能输送一种数据包,且使完成![]() 种数据包输送的数值总和最大,则下列叙述正确的序号是_______.
种数据包输送的数值总和最大,则下列叙述正确的序号是_______.
①甲线路只能输送第四种数据包;
②乙线路不能输送第二种数据包;
③丙线路可以不输送第三种数据包;
④丁线路可以输送第三种数据包;
⑤戊线路只能输送第四种数据包.
【答案】②⑤
【解析】
由表中数值可知:完成![]() 种数据包输送的数值总和最大值为:
种数据包输送的数值总和最大值为:![]() ,但不能同时取得.根据每条线路单位时间内输送不同数据包,要使总和最大,则从甲可以输送第二或第四种数据包入手,得到丙只能输送第三种数据包入丁则不可以输送第三种数据包,则丁输送第五种数据包,再对乙进行分析确定戊比较即可.
,但不能同时取得.根据每条线路单位时间内输送不同数据包,要使总和最大,则从甲可以输送第二或第四种数据包入手,得到丙只能输送第三种数据包入丁则不可以输送第三种数据包,则丁输送第五种数据包,再对乙进行分析确定戊比较即可.
由表可知:完成![]() 种数据包输送的数值总和最大值为:
种数据包输送的数值总和最大值为:
![]() ,但不能同时取得.
,但不能同时取得.
要使总和最大,甲可以输送第二或第四种数据包,丙只能输送第三种数据包,
丁则不可以输送第三种数据包,所以丁输送第五种数据包,
乙若输送第四种数据包,戊输送第一种数据包,此时,数值总和为:
![]() ,
,
乙若不输送第二种数据包,输送第一种数据包,甲输送第二种数据包,
则戊输送第四种数据包,此时,数值总和为:
![]()
所以乙不输送第二种数据包,戊输只能送第四种数据包.
故答案为:②⑤


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】![]() 年东京夏季奥运会将设置
年东京夏季奥运会将设置![]() 米男女混合泳接力这一新的比赛项目,比赛的规则是:每个参赛国家派出2男2女共计4名运动员比赛,按照仰泳
米男女混合泳接力这一新的比赛项目,比赛的规则是:每个参赛国家派出2男2女共计4名运动员比赛,按照仰泳![]() 蛙泳
蛙泳![]() 蝶泳
蝶泳![]() 自由泳的接力顺序,每种泳姿
自由泳的接力顺序,每种泳姿![]() 米且由一名运动员完成, 每个运动员都要出场. 现在中国队确定了备战该项目的4名运动员名单,其中女运动员甲只能承担仰泳或者自由泳,男运动员乙只能承担蝶泳或自由泳,剩下的男女各一名运动员则四种泳姿都可以上,那么中国队共有( )种兵布阵的方式.
米且由一名运动员完成, 每个运动员都要出场. 现在中国队确定了备战该项目的4名运动员名单,其中女运动员甲只能承担仰泳或者自由泳,男运动员乙只能承担蝶泳或自由泳,剩下的男女各一名运动员则四种泳姿都可以上,那么中国队共有( )种兵布阵的方式.
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 内有一点
内有一点![]() ,过
,过![]() 的两条直线
的两条直线![]() ,
,![]() 分别与抛物线
分别与抛物线![]() 交于
交于![]() ,
,![]() 和
和![]() ,
,![]() 两点,且满足
两点,且满足![]() ,
,![]() ,已知线段
,已知线段![]() 的中点为
的中点为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() .
.
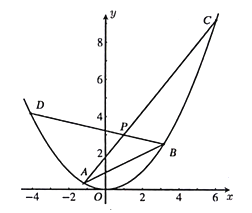
(1)求证:点![]() 的横坐标为定值;
的横坐标为定值;
(2)如果![]() ,点
,点![]() 的纵坐标小于3,求
的纵坐标小于3,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校在2016年的自主招生考试成绩中随机抽取100位学生的笔试成绩,按成绩分组,得到的频率分布表如下所示.
(1)请先求出频率分布表中①②位置相应的数据,再在答题纸上完成下列频率分布直方图(如图所示);
组号 | 分组 | 频数 | 频率 |
第1组 |
| 5 | 0.050 |
第2组 |
| ① | 0.350 |
第3组 |
| 30 | ② |
第4组 |
| 20 | 0.200 |
第5组 |
| 10 | 0.100 |
合计 | 100 | 1.000 |
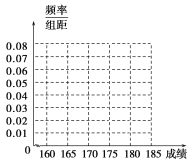
频率分布直方图
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6位学生进入第二轮面试,求第3、4、5组每组各抽取多少位学生进入第二轮面试;
(3)在(2)的前提下,学校决定在6位学生中随机抽取2位学生接受A考官进行面试,求第4组至少有一位学生被考官A面试的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,点
,点![]() 在椭圆C上,O为坐标原点.
在椭圆C上,O为坐标原点.
![]() Ⅰ
Ⅰ![]() 求椭圆C的方程;
求椭圆C的方程;
![]() Ⅱ
Ⅱ![]() 设动直线l与椭圆C有且仅有一个公共点,且l与圆
设动直线l与椭圆C有且仅有一个公共点,且l与圆![]() 的相交于不在坐标轴上的两点
的相交于不在坐标轴上的两点![]() ,
,![]() ,记直线
,记直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某产品1到6月份销售量及其价格进行调查,其售价x和销售量y之间的一组数据如下表所示:
月份i | 1 | 2 | 3 | 4 | 5 | 6 |
单价 | 9 | 9.5 | 10 | 10.5 | 11 | 8 |
销售量 | 11 | 10 | 8 | 6 | 5 | 14 |
(1)根据1至5月份的数据,求出y关于x的回归直线方程;
(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差不超过0.5元,则认为所得到的回归直线方程是理想的,试问所得到的回归直线方程是否理想?
(3)预计在今后的销售中,销售量与单价仍然服从(1)中的关系,且该产品的成本是2.5元/件,为获得最大利润,该产品的单价应定为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]()
(1)若“![]() x∈A,使得x∈B”为真命题,求m的取值范围;
x∈A,使得x∈B”为真命题,求m的取值范围;
(2)是否存在实数m,使“x∈A”是“X∈B”必要不充分条件,若存在,求出m的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题甲:对任意实数![]() ,不等式
,不等式![]() 恒成立;命题乙:已知
恒成立;命题乙:已知![]() 满足
满足![]() ,且
,且![]() 恒成立.
恒成立.
(1)分别求出甲乙为真命题时,实数![]() 的取值范围;
的取值范围;
(2)求实数![]() 的取值范围,使命题甲乙中有且只有一个真命题.
的取值范围,使命题甲乙中有且只有一个真命题.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com