
【题目】已知等比数列{an}满足a1=2,a2=4(a3﹣a4),数列{bn}满足bn=3﹣2log2an .
(1)求数列{an}和{bn}的通项公式;
(2)令cn= ![]() ,求数列{cn}的前n项和Tn;
,求数列{cn}的前n项和Tn;
(3)若λ>0,求对所有的正整数n都有2λ2﹣kλ+2>a2nbn成立的k的范围.
【答案】
(1)解:设等比数列{an}的公比为q,
∵a1=2,a2=4(a3﹣a4),
∴ ![]() ,
,
故数列{an}是以2为首项, ![]() 为公比的等比数列,
为公比的等比数列,
∵ ![]() ,
,
∴数列{bn}是首项为1,公差为2的等差数列.
∴ ![]() ;
;
(2)解:∵cn= ![]() =(2n﹣1)2n﹣2,
=(2n﹣1)2n﹣2,
∴Tn= ![]() ×1+1×3+2×5+…+2n﹣2×(2n﹣1),
×1+1×3+2×5+…+2n﹣2×(2n﹣1),
![]() ,
,
两式相减得: ![]()
= ![]() ,
,
∴ ![]() ;
;
(3)解:由(1)知 ![]() ,
,
∴数列{a2nbn}为单调递减数列;
∴当n≥1时, ![]() ,即a2nbn最大值为1,
,即a2nbn最大值为1,
由2λ2﹣kλ+2>1可得 ![]() ,
,
而当λ>0时, ![]() ,当且仅当
,当且仅当 ![]() 时取等号,
时取等号,
∴ ![]() .
.
【解析】(1)通过设等比数列{an}的公比为q,通过a1=2、a2=4(a3﹣a4)计算可知数列{an}是以2为首项、 ![]() 为公比的等比数列,进而数列{bn}是首项为1、公差为2的等差数列,计算即得结论;(2)通过(1)可知cn=(2n﹣1)2n﹣2 , 利用错位相减法计算即得结论;(3)通过(1)知数列{a2nbn}为单调递减数列,进而只需解不等式2λ2﹣kλ+2>a2b1 , 利用基本不等式计算即得结论.
为公比的等比数列,进而数列{bn}是首项为1、公差为2的等差数列,计算即得结论;(2)通过(1)可知cn=(2n﹣1)2n﹣2 , 利用错位相减法计算即得结论;(3)通过(1)知数列{a2nbn}为单调递减数列,进而只需解不等式2λ2﹣kλ+2>a2b1 , 利用基本不等式计算即得结论.
【考点精析】根据题目的已知条件,利用等比数列的通项公式(及其变式)和数列的前n项和的相关知识可以得到问题的答案,需要掌握通项公式:![]() ;数列{an}的前n项和sn与通项an的关系
;数列{an}的前n项和sn与通项an的关系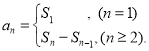 .
.


科目:高中数学 来源: 题型:
【题目】设数列{an},a1=1,an+1= ![]() +
+ ![]() ,数列{bn},bn=2n﹣1an .
,数列{bn},bn=2n﹣1an .
(1)求证:数列{bn}为等差数列,并求出{bn}的通项公式;
(2)数列{an}的前n项和为Sn , 求Sn;
(3)正数数列{dn}满足 ![]() =
= ![]() .设数列{dn}的前n项和为Dn , 求不超过D100的最大整数的值.
.设数列{dn}的前n项和为Dn , 求不超过D100的最大整数的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:x2+mx+1=0有两个不等的负根;命题q:4x2+4(m﹣2)x+1=0无实根.若命题p与命题q有且只有一个为真,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,为了测量正在海面匀速行驶的某船的速度,在海岸上选取距离1千米的两个观察
点C、D,在某天10:00观察到该船在A处,此时测得∠ADC=30°,2分钟后该船行驶至B处,此时测得∠ACB=60°,∠BCD=45°,∠ADB=60°,
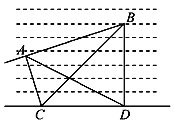
求该船航行的速度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱ABCD﹣A1B1C1D1中,底面四边形ABCD是直角梯形,其中AB⊥AD,AB=BC=1且AD= ![]() AA1=2.
AA1=2. 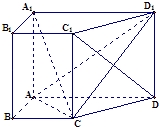
(1)求证:直线C1D⊥平面ACD1;
(2)试求三棱锥A1﹣ACD1的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(wx+φ)(x∈R,w>0,0<φ< ![]() )的部分图象如图所示.
)的部分图象如图所示. 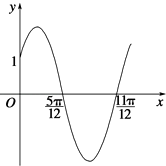
(1)求函数f(x)的解析式;
(2)求函数g(x)=f(x﹣ ![]() )﹣f(x+
)﹣f(x+ ![]() )的单调递增区间.
)的单调递增区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com