
【题目】已知函数![]() .
.
(1)求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)设 ,计算
,计算![]() 的导数.
的导数.
【答案】(1)![]() .(2)
.(2) .
.
【解析】试题分析:(1)由导数的基本定义就出斜率,根据点斜式写出切线方程![]() ;(2)
;(2)![]() ,
,  .
.
试题解析:
(1)![]() ,则
,则![]() ,
,
又![]() ,∴所求切线方程为
,∴所求切线方程为![]() ,即
,即![]() .
.
(2)![]() ,
,  .
.
【题型】解答题
【结束】
18
【题目】对某校高一年级学生参加社区服务次数进行统计,随机抽取![]() 名学生作为样本,得到这
名学生作为样本,得到这![]() 名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:

(1)求出表中![]() 及图中
及图中![]() 的值;
的值;
(2)若该校高一学生有800人,试估计该校高一学生参加社区服务的次数在区间![]() 内的人数.
内的人数.
科目:高中数学 来源: 题型:
【题目】某工厂生产一种仪器的元件,由于受生产能力和技术水平的限制,会产生一些次品,根据经验知道,其次品率P与日产量x(万件)之间大体满足关系:  (其中c为小于6的正常数). (注:次品率=次品数/生产量,如P=0.1表示每生产10件产品,有1件为次品,其余为合格品),已知每生产1万件合格的元件可以盈利2万元,但每生产出1万件次品将亏损1万元,故厂方希望定出合适的日产量.
(其中c为小于6的正常数). (注:次品率=次品数/生产量,如P=0.1表示每生产10件产品,有1件为次品,其余为合格品),已知每生产1万件合格的元件可以盈利2万元,但每生产出1万件次品将亏损1万元,故厂方希望定出合适的日产量.
(1)试将生产这种仪器的元件每天的盈利额T(万元)表示为日产量x(万件)的函数;
(2)当日产量为多少时,可获得最大利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,平行四边形ABCD中,AB=2AD,∠DAB=60°,M是BC的中点.将△ADM沿DM折起,使面ADM⊥面MBCD,N是CD的中点,图2所示. 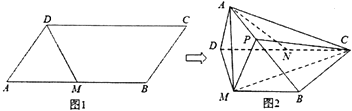
(Ⅰ)求证:CM⊥平面ADM;
(Ⅱ)若P是棱AB上的动点,当 ![]() 为何值时,二面角P﹣MC﹣B的大小为60°.
为何值时,二面角P﹣MC﹣B的大小为60°.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△ABC和△ACD中,∠ACB=∠ADC=90°,∠BAC=∠CAD,⊙O是以AB为直径的圆,DC的延长线与AB的延长线交于点E.
(Ⅰ)求证:DC是⊙O的切线;
(Ⅱ)若EB=6,EC=6 ![]() ,求BC的长.
,求BC的长.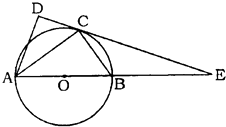
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为减少空气污染,某市鼓励居民用电(减少燃气或燃煤),采用分段计费的方法计算电费每月用电不超过100度仍按原标准收费,超过的部分每度按0.5元计算.
Ⅰ.设月用电x度时,应交电费y元,写出y关于x的函数关系式;
Ⅱ.小明家第一季度缴纳电费情况如下:
月份 | 一月 | 二月 | 三月 | 合计 |
缴费金额 | 76元 | 63元 | 45.6元 | 184.6元 |
问小明家第一季度共用多少度?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:y=﹣x+1与椭圆C: ![]() =1(a>b>0))相交于不同的两点A、B,且线段AB的中点P的坐标为(
=1(a>b>0))相交于不同的两点A、B,且线段AB的中点P的坐标为( ![]() ,
, ![]() )
) 
(1)求椭圆C离心率;
(2)设O为坐标原点,且2|OP|=|AB|,求椭圆C的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某石化集团获得了某地深海油田区块的开采权,集团在该地区随机初步勘探了部分几口井,取得了地质资料.进入全面勘探时期后,集团按网络点来布置井位进行全面勘探,由于勘探一口井的费用很高,如果新设计的井位与原有井位重合或接近,便利用旧井的地质资料,不必打这口新井,以节约勘探费用,勘探初期数据资料见如表:
井号 | 1 | 2 | 3 | 4 | 5 | 6 |
坐标 |
|
|
|
|
|
|
钻探深度( | 2 | 4 | 5 | 6 | 8 | 10 |
出油量( | 40 | 70 | 110 | 90 | 160 | 205 |
(参考公式和计算结果:  ,
, ![]() ,
, ![]() ,
, ![]() )
)
(1)![]() 号旧井位置线性分布,借助前
号旧井位置线性分布,借助前![]() 组数据求得回归直线方程为
组数据求得回归直线方程为![]() ;求
;求![]() ,并估计
,并估计![]() 的预报值;
的预报值;
(2)现准备勘探新井![]() ,若通过1,3,5,7号并计算出的
,若通过1,3,5,7号并计算出的![]() ,
, ![]() 的值(
的值(![]() ,
, ![]() 精确到
精确到![]() )相比于(1)中的
)相比于(1)中的![]() ,
, ![]() ,且
,且![]() ,则使用位置最接近的已有旧井
,则使用位置最接近的已有旧井![]() ,否则在新位置打开,请判断可否使用旧井?
,否则在新位置打开,请判断可否使用旧井?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com