
【题目】已知a,b,c为△ABC的内角A,B,C的对边,满足 ![]() =
= ![]() ,函数f(x)=sinωx(ω>0)在区间[0,
,函数f(x)=sinωx(ω>0)在区间[0, ![]() ]上单调递增,在区间[
]上单调递增,在区间[ ![]() ,π]上单调递减.
,π]上单调递减.
(1)证明:b+c=2a;
(2)若f( ![]() )=cos A,试判断△ABC的形状.
)=cos A,试判断△ABC的形状.
【答案】
(1)证明:∵ ![]() ,
,
∴sinBcosA+sinCcosA=2sinA﹣cosBsinA﹣cosCsinA
化简得sin(B+A)+sin(C+A)=2sinA,
由A+B+C=π,则sinC+sinB=2sinA,
由正弦定理得,b+c=2a
(2)解:∵f(x)=sinωx(ω>0)在[0, ![]() ]上递增,在[
]上递增,在[ ![]() ,π]上递减,
,π]上递减,
∴ ![]() ,则T=
,则T= ![]() =
= ![]() ,解得ω=
,解得ω= ![]() ,
,
则f(x)=sin ![]() ,
,
∴f( ![]() )=sin(
)=sin( ![]() )=sin
)=sin ![]() =cos A,则cos A=
=cos A,则cos A= ![]() ,
,
又b+c=2a,由余弦定理得a2=b2+c2﹣2bccosA,
∴a2=(b+c)2﹣3bc,则a2=bc,
联立b+c=2a得,b=c=a,
∴△ABC是等边三角形
【解析】(1)根据两角和的正弦公式、诱导公式化简已知的式子,由正弦定理可得b+c=2a;(2)根据题意和正弦函数的单调性求出周期,由周期公式求出ω的值,化简f( ![]() )=cos A,求出cos A的值,利用条件和余弦定理列出方程,化简后联立方程求出a、b、c的关系,可判断出△ABC的形状.
)=cos A,求出cos A的值,利用条件和余弦定理列出方程,化简后联立方程求出a、b、c的关系,可判断出△ABC的形状.
【考点精析】掌握余弦定理的定义是解答本题的根本,需要知道余弦定理:![]() ;
;![]() ;
;![]() .
.


科目:高中数学 来源: 题型:
【题目】某企业生产一种机器的固定成本为0.5万元,但每生产1百台时,又需可变成本(即另增加投入)0.25万元.市场对此商品的年需求量为5百台,销售的收入(单位:万元)函数为:R(x)=5x﹣ ![]() x2(0≤x≤5),其中x是产品生产的数量(单位:百台).
x2(0≤x≤5),其中x是产品生产的数量(单位:百台).
(1)将利润表示为产量的函数;
(2)年产量是多少时,企业所得利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标标系xoy中,已知曲线 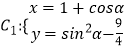 (α为参数,α∈R),在以原点O为极点,x轴非负半轴为极轴的极坐标系中(取相同的长度单位),曲线
(α为参数,α∈R),在以原点O为极点,x轴非负半轴为极轴的极坐标系中(取相同的长度单位),曲线 ![]() =
= ![]() ,曲线C3:ρ=2cosθ. (Ⅰ)求曲线C1与C2的交点M的直角坐标;
,曲线C3:ρ=2cosθ. (Ⅰ)求曲线C1与C2的交点M的直角坐标;
(Ⅱ)设A,B分别为曲线C2 , C3上的动点,求|AB|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】和谐高级中学共有学生570名,各班级人数如表:
一班 | 二班 | 三班 | 四班 | |
高一 | 52 | 51 | y | 48 |
高二 | 48 | x | 49 | 47 |
高三 | 44 | 47 | 46 | 43 |
已知在全校学生中随机抽取1名,抽到高二年级学生的概率是 ![]() .
.
(1)求x,y的值;
(2)现用分层抽样的方法在全校抽取114名学生,应分别在各年级抽取多少名?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且满足a1=3,Sn+1=3(Sn+1)(n∈N*). (Ⅰ)求数列{an}的通项公式;
(Ⅱ)在数列{bn}中,b1=9,bn+1﹣bn=2(an+1﹣an)(n∈N*),若不等式λbn>an+36(n﹣4)+3λ对一切n∈N*恒成立,求实数λ的取值范围;
(Ⅲ)令Tn= ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() (n∈N*),证明:对于任意的n∈N* , Tn<
(n∈N*),证明:对于任意的n∈N* , Tn< ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com