
(本小题满分12分) 已知圆 ,点
,点 ,直线
,直线 .
.
(1) 求与圆 相切,且与直线
相切,且与直线 垂直的直线方程;
垂直的直线方程;
(2) 在直线 上(
上( 为坐标原点),存在定点
为坐标原点),存在定点 (不同于点
(不同于点 ),满足:对于圆
),满足:对于圆 上任一点
上任一点 ,都有
,都有 为一常数,试求所有满足条件的点
为一常数,试求所有满足条件的点 的坐标.
的坐标.
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:高中数学 来源: 题型:解答题
已知圆 的方程为
的方程为 ,直线
,直线
 ,设点
,设点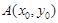 .
.
(1)若点 在圆
在圆 外,试判断直线
外,试判断直线 与圆
与圆 的位置关系;
的位置关系;
(2)若点 在圆
在圆 上,且
上,且 ,
, ,过点
,过点 作直线
作直线 分别交圆
分别交圆 于
于 两点,且直线
两点,且直线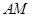 和
和 的斜率互为相反数;
的斜率互为相反数;
① 若直线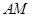 过点
过点 ,求
,求 的值;
的值;
② 试问:不论直线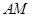 的斜率怎样变化,直线
的斜率怎样变化,直线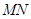 的斜率是否为定值?若是,求出该定值;若不是,说明理由.
的斜率是否为定值?若是,求出该定值;若不是,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com