
| 年份 | 1972 | 1976 | 1980 | 1984 | 1988 | 1992 | 1996 | 2000 | 2004 | 2008 |
| 届别 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 主办国家 | 联邦德国 | 加拿大 | 苏联 | 美国 | 韩国 | 西班牙 | 美国 | 澳大利亚 | 希腊 | 中国 |
| 上届金牌数 | 5 | 0 | 49 | 未参加 | 6 | 1 | 37 | 9 | 4 | 32 |
| 当界金牌数 | 13 | 0 | 80 | 83 | 12 | 13 | 44 | 16 | 6 | 51 |
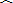 |
| y |
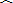 |
| b |
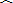 |
| a |
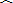 |
| b |
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
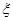 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求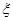 的分布列和数学期望
的分布列和数学期望查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
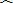 |
| y |
| |||||||
|
| |||||||
|
| . |
| y |
| . |
| x |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
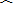 |
| y |
| A.在(-1,0)内 | B.在(-1,1)内 | C.在(0,1)内 | D.在[1,+∞)内 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.y=0.8x+3 | B.y=-1.2x+7.5 |
| C.y=1.6x+0.5 | D.y=1.3x+1.2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 |
| y |
 |
| y |
 |
| y |
 |
| y |
| A.①② | B.②③ | C.③④ | D.①④ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 |
| y |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 日期 | 1月10日 | 2月10日 | 3月10日 | 4月10日 | 5月10日 | 6月10日 |
| 昼夜温差x(℃) | 10 | 11 | 13 | 12 | 8 | 6 |
| 就诊人数y(人) | 22 | 25 | 29 | 26 | 16 | 12 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 使用年限x | 2 | 3 | 4 | 5 | 6 |
| 总费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
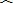 |
| y |
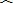 |
| b |
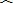 |
| a |
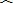 |
| a |
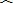 |
| b |
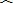 |
| b |
| |||||
|
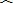 |
| a |
| . |
| y |
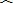 |
| b |
| . |
| x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com