解:(1)由

知四边形PF
1OM为平行四边形,
又由

知OP平分∠F
1OM,∴PF
1OM为菱形,
设半焦距为c,由
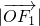
=c 知

=c,

,∴

,
又

,即
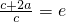
e
2-e-2=0,∴e=2(e=-1舍去)(4分)
(2)∵e=2=

∴c=2a,∴双曲线方程为
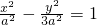
,
将点(2,

)代入,有

∴a
2=3.
即所求双曲线方程为
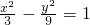
.(8分)
(3)依题意得B
1(0,3),B
2(0,-3)
设直线AB的方程为y=kx-3,A(x
1,y
1)B(x
2,y
2).
则由

.
∵双曲线的渐近线为y=±

x,∴k=±

时,AB与双曲线只有一个交点,
即k≠±

∵x
1+x
2=-
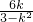
,x
1•x
2=
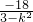
.
y
1+y
2=k(x
1+x
2)-6=
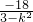
,y
1y
2=k
2x
1x
2-k(x
1+x
2)+9=9
又
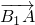
=(x
1,y
1-3),
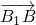
=(x
2,y
2-3),
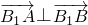
?x
1x
2+y
1y
2-3(y
1+y
2)+9=0,
∴

,即k
2=5∴k=±

.
故所求直线AB的方程为y=

x-3或y=-

x-3.(14分)
分析:(1)先由

知四边形PF
1OM为平行四边形,再利用

得PF
1OM为菱形,所以就有
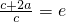
求出离心率e即可.
(2)由(1)求出的离心率e以及双曲线过点N(2,

),可以求出c,a进而求出双曲线方程;
(3)先设出直线AB的方程,再与双曲线方程联立,求出关于A,B两点坐标的方程,再利用
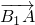
⊥
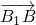
?x
1x
2+y
1y
2-3(y
1+y
2)+9=0,就可求出对应的直线的斜率,进而求出直线AB的方程.
点评:本题综合考查了直线与椭圆的位置关系以及向量共线问题.直线与圆锥曲线的位置关系,由于集中交汇了直线,圆锥曲线两章的知识内容,综合性强,能力要求高,还涉及到函数,方程,不等式,平面几何等许多知识,可以有效的考查函数与方程的思想,数形结合的思想,分类讨论的思想和转化化归的思想,因此,这一部分内容也成了高考的热点和重点.

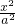 -
- =1的左右焦点,O为坐标原点,P在双曲线左支上,M在右准线上,且满足
=1的左右焦点,O为坐标原点,P在双曲线左支上,M在右准线上,且满足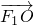 =
=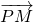 ,
,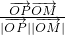 =
=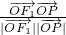
 ),求双曲线方程;
),求双曲线方程;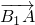 ⊥
⊥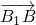 时,直线AB的方程.
时,直线AB的方程. 知四边形PF1OM为平行四边形,
知四边形PF1OM为平行四边形,
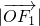 =c 知
=c 知 =c,
=c, ,∴
,∴ ,
, ,即
,即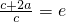
 ∴c=2a,∴双曲线方程为
∴c=2a,∴双曲线方程为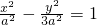 ,
, )代入,有
)代入,有 ∴a2=3.
∴a2=3.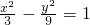 .(8分)
.(8分) .
. x,∴k=±
x,∴k=± 时,AB与双曲线只有一个交点,
时,AB与双曲线只有一个交点, ∵x1+x2=-
∵x1+x2=-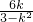 ,x1•x2=
,x1•x2=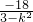 .
.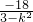 ,y1y2=k2x1x2-k(x1+x2)+9=9
,y1y2=k2x1x2-k(x1+x2)+9=9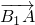 =(x1,y1-3),
=(x1,y1-3),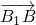 =(x2,y2-3),
=(x2,y2-3),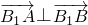 ?x1x2+y1y2-3(y1+y2)+9=0,
?x1x2+y1y2-3(y1+y2)+9=0, ,即k2=5∴k=±
,即k2=5∴k=± .
. x-3或y=-
x-3或y=- x-3.(14分)
x-3.(14分) 知四边形PF1OM为平行四边形,再利用
知四边形PF1OM为平行四边形,再利用 得PF1OM为菱形,所以就有
得PF1OM为菱形,所以就有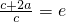
 ),可以求出c,a进而求出双曲线方程;
),可以求出c,a进而求出双曲线方程;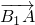 ⊥
⊥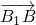 ?x1x2+y1y2-3(y1+y2)+9=0,就可求出对应的直线的斜率,进而求出直线AB的方程.
?x1x2+y1y2-3(y1+y2)+9=0,就可求出对应的直线的斜率,进而求出直线AB的方程.

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案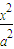 -
- =1的左右焦点,O为坐标原点,P在双曲线左支上,M在右准线上,且满足
=1的左右焦点,O为坐标原点,P在双曲线左支上,M在右准线上,且满足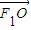 =
=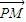 ,
,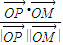 =
=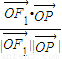
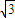 ),求双曲线方程;
),求双曲线方程;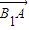 ⊥
⊥ 时,直线AB的方程.
时,直线AB的方程. -
- =1的左右焦点,O为坐标原点,P在双曲线左支上,M在右准线上,且满足
=1的左右焦点,O为坐标原点,P在双曲线左支上,M在右准线上,且满足 =
= ,
, =
=
 ),求双曲线方程;
),求双曲线方程; ⊥
⊥ 时,直线AB的方程.
时,直线AB的方程.