
【题目】已知函数![]() ;
;
![]() 讨论
讨论![]() 的极值点的个数;
的极值点的个数;
![]() 若
若![]() ,求证:
,求证:![]() .
.
【答案】(1)当a≤0时,f(x)无极值点;当a>0时,函数y=f(x)有一个极大值点,无极小值点;(2)见解析
【解析】
:(1)先求一阶导函数![]() 的根,求解
的根,求解![]() 或
或![]() 的解集,写出单调区间,最后判断极值点。
的解集,写出单调区间,最后判断极值点。
(2)根据第(1)问的结论,若![]() ,转化为证明
,转化为证明![]() .
.
:(1)根据题意可得,![]() ,
,
当![]() 时,
时,![]() ,函数
,函数![]() 是减函数,无极值点;
是减函数,无极值点;
当![]() 时,令
时,令![]() ,得
,得![]() ,即
,即![]() ,
,
又![]() 在
在![]() 上存在一解,不妨设为
上存在一解,不妨设为![]() ,
,
所以函数![]() 在
在![]() 上是单调递增的,在
上是单调递增的,在![]() 上是单调递减的.
上是单调递减的.
所以函数![]() 有一个极大值点,无极小值点;
有一个极大值点,无极小值点;
总之:当![]() 时,无极值点;
时,无极值点;
当![]() 时,函数
时,函数![]() 有一个极大值点,无极小值点.
有一个极大值点,无极小值点.
(2)![]() ,
,![]() ,
,
由(1)可知![]() 有极大值
有极大值![]() ,且
,且![]() 满足
满足![]() ①,
①,
又![]() 在
在![]() 上是增函数,且
上是增函数,且![]() ,所以
,所以![]() ,
,
又知:![]() ,②
,②
由①可得![]() ,代入②得
,代入②得![]() ,
,
令![]() ,则
,则![]() 恒成立,
恒成立,
所以![]() 在
在![]() 上是增函数,
上是增函数,
所以![]() ,即
,即![]() ,
,
所以![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】(本大题满分12分)
随着互联网的快速发展,基于互联网的共享单车应运而生,某市场研究人员为了了解共享单车运营公司![]() 的经营状况,对该公司最近六个月的市场占有率进行了统计,并绘制了相应的折线图:
的经营状况,对该公司最近六个月的市场占有率进行了统计,并绘制了相应的折线图:
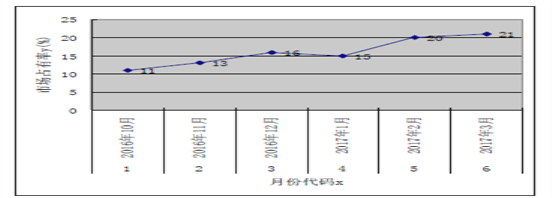
(Ⅰ)由折线图可以看出,可用线性回归模型拟合月度市场占有率![]() 与月份代码
与月份代码![]() 之间的关系,求
之间的关系,求![]() 关于
关于![]() 的线性回归方程,并预测
的线性回归方程,并预测![]() 公司2017年4月的市场占有率;
公司2017年4月的市场占有率;
(Ⅱ)为进一步扩大市场,公司拟再采购一批单车,现有采购成本分别为![]() 元/辆和1200元/辆的
元/辆和1200元/辆的![]() 、
、![]() 两款车型可供选择,按规定每辆单车最多使用4年,但由于多种原因(如骑行频率等)会导致单车使用寿命各不相同,考虑到公司运营的经济效益,该公司决定先对这两款车型的单车各100辆进行科学模拟测试,得到两款单车使用寿命的频数表如下:
两款车型可供选择,按规定每辆单车最多使用4年,但由于多种原因(如骑行频率等)会导致单车使用寿命各不相同,考虑到公司运营的经济效益,该公司决定先对这两款车型的单车各100辆进行科学模拟测试,得到两款单车使用寿命的频数表如下:
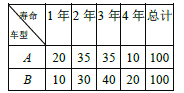
经测算,平均每辆单车每年可以带来收入500元,不考虑除采购成本之外的其他成本,假设每辆单车的使用寿命都是整数年,且以频率作为每辆单车使用寿命的概率,如果你是![]() 公司的负责人,以每辆单车产生利润的期望值为决策依据,你会选择采购哪款车型?
公司的负责人,以每辆单车产生利润的期望值为决策依据,你会选择采购哪款车型?
参考公式:回归直线方程为![]() ,其中
,其中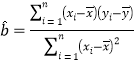 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 设命题p:函数y=![]() 在定义域上为减函数;命题q:a,b∈(0,+∞),当a+b=1时,
在定义域上为减函数;命题q:a,b∈(0,+∞),当a+b=1时,![]() +
+![]() =3.以下说法正确的是( )
=3.以下说法正确的是( )
A. p∨q为真B. p∧q为真
C. p真q假D. p,q均假
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一年级共有![]() 名学生,其中男生
名学生,其中男生![]() 名,女生
名,女生![]() 名,该校组织了一次口语模拟考试(满分为
名,该校组织了一次口语模拟考试(满分为![]() 分).为研究这次口语考试成绩为高分是否与性别有关,现按性别采用分层抽样抽取
分).为研究这次口语考试成绩为高分是否与性别有关,现按性别采用分层抽样抽取![]() 名学生的成绩,按从低到高分成
名学生的成绩,按从低到高分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 七组,并绘制成如图所示的频率分布直方图.已知
七组,并绘制成如图所示的频率分布直方图.已知![]() 的频率等于
的频率等于![]() 的频率,
的频率,![]() 的频率与
的频率与![]() 的频率之比为
的频率之比为![]() ,成绩高于
,成绩高于![]() 分的为“高分”.
分的为“高分”.
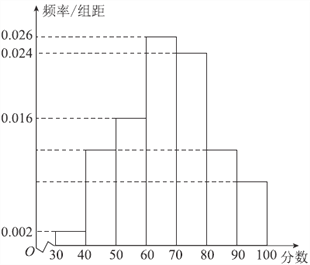
(1)估计该校高一年级学生在口语考试中,成绩为“高分”的人数;
(2)请你根据已知条件将下列![]() 列联表补充完整,并判断是否有
列联表补充完整,并判断是否有![]() 的把握认为“该校高一年级学生在本次口语考试中成绩及格(
的把握认为“该校高一年级学生在本次口语考试中成绩及格(![]() 分以上(含
分以上(含![]() 分)为及格)与性别有关”?
分)为及格)与性别有关”?
口语成绩及格 | 口语成绩不及格 | 合计 | |
男生 |
|
| |
女生 |
|
| |
合计 |
|
附临界值表:
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com